A Game-based Thermal-aware Resource Allocation
Strategy for Data Centers
1
Saeed Akbar,
2Saif Ur Rehman Malik,
3Kim-Kwang Raymond Choo,
4Samee U. Khan,
5Naveed Ahmad,
6Adeel
Anjum
Abstract—Data centers (DC) host a large number of servers, computing devices and computing infrastructure, and hence incur significant amount of electricity / energy. This also results in high amount of heat produced, which if not addressed can lead to over-heating of computing devices in the DC. In addition, temperature mismanagement can lead to thermal imbalance within the DC environment, which may result in the creation of hotspots. The energy consumed during the life of a hotspot is greater than the energy saved during computation. Hence, the thermal imbalance impacts on the efficiency of the cooling mechanism installed inside the DC, and the consequence is high energy consumption. One popular strategy to minimize energy consumption is to optimize resource allocation within the DC. However, existing scheduling strategies do not consider the ambient effect of the surrounding nodes at the time of job allocation. Moreover, thermal-aware resource scheduling as an optimization problem is a topic that is relatively understudied in the literature. Therefore, in this research, we propose a novel Game-based Thermal-Aware Resource Allocation (GTARA) strategy to reduce the thermal imbalance within the DC. Specifically, we use cooperative game theory with a Nash-bargaining solution concept to model the resource allocation as an optimization problem, where user jobs are assigned to the computing nodes based on their thermal profiles and their potential effect on the surrounding nodes. This allows us to improve thermal balance and avoid hotspots. We then demonstrate the effectiveness of GTARA in comparison to TACS (Thermal-aware Control Strategy), TASA (Thermal-aware Scheduling Algorithm) and FCFS (First-Come First-Served), in terms of minimizing thermal imbalance and hotspots.
Index Terms—Resource Allocation, Cloud Computing, Data Center, Cooperative Game Theory.
I. INTRODUCTION
Data Centers (DC) are crucial infrastructure in empower-ing Internet-based services. The DC generally host a large number of computing and storage systems and devices (e.g. servers and other networking equipment). To fulfill the user demands, the number of servers hosted by the DC is increasing exponentially. Consequently, the energy consumed by the DC worldwide is increasing with tremendous speed. The energy cost of the DC is nearly equal to their infrastructure cost [1].
1Saeed Akbar, is with the Department of Computer Science, IQRA National University, Peshawar, Pakistan.
2Saif U. R. Malik, is with Department of Computer Science, COMSATS University, Islamabad Pakistan and Cybernetica AS, Estonia.
3Kim-Kwang Raymond Choo, is with Department of Information Systems and Cyber Security, University of Texas at San Antonio, 12346 San Antonio, Texas United States 78249-1644.
4Samee U. Khan, is with Department of Electrical and Computer Engi-neering, North Dakota State University, Fargo, North Dakota United States 58108-6050.
5Naveed Ahmad and6Adeel Anjum, are with Department of Computer Science, COMSATS University, Islamabad, Pakistan.
The servers consume 80% of the total energy consumed by the infrastructure components [2]. A large amount of heat produced due to the high energy consumption can result in overheating of the computing and storage devices within the DC. Moreover, the arrangement of the servers within the DC is very compact [3], which also contributes to the increase in server’s temperature due to the ambient effect of the surrounding servers. To guarantee the normal operation and reliability of the DC equipment, cooling mechanisms are installed inside the DC environment. A significant amount of energy is required for the cooling system to keep the servers and other necessary DC equipment under the vendor specified threshold temperature.
Without proper management, the DC can lead to thermal imbalance and hotspots. Moreover, according to [4], during the life of a hotspot, more energy is consumed for cooling as compared to the energy saved during computation. Further-more, the hotspots can lead to failure of the hardware and end up with degraded performance. Hence, violating the service-level agreements with the customers/users [5]. A Tremendous amount of energy can be saved if we reduce the energy con-sumed for the cooling purposes inside the DC. The resource scheduling algorithms can help reduce energy consumption and make the DC more cost-efficient [6]. For example, the study in [7] demonstrated that the energy consumed by the DC worldwide has been significantly reduced by employing efficient resource allocation mechanisms. The Thermal-Aware (TA) resource scheduling is one of the several strategies to help reduce the thermal imbalances and hotspots within the DC.
The TA task allocation is the distribution of workload based on the thermal profiles of the computing nodes and the tasks. The TA resource allocation strategies aim at minimizing the power consumption by achieving thermal uniformity in the DC environment. Moreover, the TA job allocation strategy can result in the following benefits: (1) reduced cooling costs [8]; (2) improved operations and increased reliability of the DC equipment [9]. In this work, our goal is to devise a novel software driven TA strategy to optimize thermal uniformity in the DC. Moreover, to achieve the stated goal, we will model the job scheduling process in the DC as an optimization problem using Game Theory.
Game theory (GT) is used to model the strategic interactions among rational and self-interested agents. Based on the current strategies and conditions of the environment, it studies the optimal behavior of those agents. So, in an environment where the decision of one agent is dependent on the decisions of the
other agents, the GT is a very useful tool in order to analyze the outcomes of the decisions taken by the agents. Applying GT to the task scheduling problems is a new research area and will lead to better outcomes in terms of energy efficiency [10].
Resource allocation can be considered as an optimization problem. However, the modeling of the DC scheduling as an optimization problem appears to be an understudied topic in the literature. Moreover, the thermal uniformity achieved using the classical TA strategies can be further optimized using the GT [10]. Therefore, we propose using Cooperative Game Theory (CGT) to model and optimize the job allocation problem in DCs..
Contributions: In this paper, we propose a Game-based Thermal-Aware Resource Allocation (GTARA) strategy, which models the resource allocation process using CGT to minimize thermal imbalance within DCs. By assigning the “hottest” (temperature) job to the coolest node and considering ambient effect of the surrounding nodes, we are able to achieve better thermal uniformity while reducing the need for job migration. The contributions are summarized as follow:
• Resource allocation in DCs is modeled as an optimization
problem using CGT.
• Ambient effect of surrounding nodes is considered while
assigning jobs to the computing nodes.
• A comparative analysis of the proposed solution with
existing scheduling strategies is performed, and the sim-ulation results show that GTARA outperforms its com-petitors, in terms of thermal balance and the number of hotspots and migrations.
The remaining sections of the paper are organized as: section 2 covers the literature review of the TA job scheduling algorithms; section 3 introduces the game theoretic model of the DC scheduling problem; section 4 describes the proposed game theoretic approach; section 5 discusses the simulation results and briefly describes the dataset used; and finally, section 6 presents the conclusion.
II. RELATEDWORK
The high energy consumption of the DC is due to the following two reasons: energy consumed by the servers, and energy consumed by the cooling mechanisms to keep the DC environment cool. To reduce the energy consumption inside DC, numerous resource allocation strategies have been proposed in the literature. We divide these techniques into two main categories: (1) Game theoretic Approaches and (2) Classical Approaches (which do not use game theory).
A. Classical Approaches
The classical approaches can be further classified into the following sub-categories: TA strategies, DC design strategies, economization, and air-flow management [11]. Our focus, in this paper, is on the TA job scheduling. Several TA strategies have been proposed in the literature. For instance, the strate-gies proposed in [12] are based on the random selection of nodes and are aimed at minimizing the heat recirculation and the cooling cost of the DC. However, the random selection
may lead to a situation where the same node is selected: which results in the thermal imbalances and the creation of hot-spots. A logical thermal topology has been proposed in [13] that focuses on the thermal efficient workload placement. However, it neglects the servers’ temperatures crossing the red-line values. In [14], the authors proposed a reactive approach for achieving a uniform servers outlet temperature in the DC by allocating the workload to the servers having the lowest inlet temperatures. To keep the servers’ outlet temperatures homogeneous, [15] proposed Uniform Outlet Profile (UOP), a TA scheduling algorithm. The main tasks are divided into subtasks and the total power consumption by those tasks is calculated. Then the subtasks are assigned to the servers based on the thermodynamic model to keep the outlet temperatures of all the servers at a homogeneous level. However, the limitation of this method is that the tasks may not be divided into the subtasks and requires detailed knowledge of the power consumption when a server executes the task [3].
The scheduling approach proposed in [16] assigns the less CPU intensive tasks to the low-frequency processors. An approach proposed in [17] introduces idle CPU cycles in the job scheduling process to minimize the temperature of a system. This results in performance degradation [18] and slow execution of the jobs due to which the jobs may not complete within the deadline. Wang et al. [19] introduced a proactive strategy based on the thermal profiling where the hottest jobs are scheduled first and the servers are sorted in ascending order of their temperatures. The thermal profile (TP) is used to predict the temperature of a server if a certain job is to run on that particular server. This helps in keeping the temperature of the server under the threshold value and hence, the cooling cost is reduced. However, the drawbacks are: it requires the servers to be homogeneous as heat produced due the job running on heterogeneous servers is different, and it may lead to longer response time of the jobs [3]. Ref. [20] presents a mechanism to avoid hot-spots. The proposed approach defines a threshold temperature of the servers and does migrations to avoid hot-spots when the threshold temperature is reached. The proposed method is efficient in tackling the hot-spots creation. However, thermal imbalances may arise which is not considered by the proposed methodology. A VM allocation mechanism based on the thermal profiles of the hosts is proposed in [21] to reduce the power consumption. The proposed mechanism reduces the energy consumption significantly with low VM migrations while not violating the SLAs.
Two TA schemes are introduced in [22] that distributes the workload based on the TP. The proposed algorithm achieves better results in terms of temperature drop as compared to its competitors. However, the distribution of the workload is at the rack level and it does not consider avoiding hotspots and achieving thermal balance in the DC environment. In [8], the authors have theoretically analyzed the energy minimization considering the air-flow recirculation. The optimization theory is combined with the controller design to study the DC and their thermodynamics. They showed how to distribute the workload optimally and achieve the optimal cooling tem-perature while keeping the temtem-perature of the computing nodes under the threshold value and the processing of jobs
is satisfactory.
In [23], the authors present a two-time-scale control (TTSC) to reduce the power consumption inside the DC. It coordinates the DVFS, the TA task allocation, and the cooling mechanism. Results show that, compared to other methods, the TTSC is efficient in terms of power consumption. However, the proposed method is not suitable for delay sensitive tasks. A thermal-aware VM consolidation (VMAP+) is proposed in [24]. It is a proactive approach which aims at achieving thermal balance in the DC and hence, minimizing energy consumption. As compared to the ”best fit” and the ”cool job” approach, the VMAP+ is better in minimizing the energy consumption and the resource utilization while keeping the temperature under the threshold value. However, the proposed method depends on the accuracy of prediction; in the case of misprediction, the thermal imbalance may occur which will result in the hotspots and more energy will be consumed by the cooling mechanism.
In [25], wang et al. presents a Thermal-Aware Scheduling Algorithm (TASA) which assigns the hottest jobs to the coolest servers. However, the proposed scheme does not take any remedial action in the case when the threshold temperature is reached. In [26], the authors present a scheduling algorithm to achieve thermal balance and avoid hot-spots using multi-level perceptrons for prediction. The model is dynamic and updated by the input data from sensors. The problem with this solution is when misprediction occurs; it might result in the thermal imbalances and hot-spots which will cause significant power consumption.
B. Game Theoretic Approaches
The GT has been widely used to study and model decision-making problems in any domain where multiple self-interested agents are involved. Similarly, the GT has been extensively uti-lized to solve various problems in the field of cloud computing. A huge amount of literature exists that uses the GT to solve the load balancing problems in the distributed systems and the DC. In [27], the non-cooperative game has been used to model the system in order to reduce the power consumption. In [28], the authors proposed a scheme based on the non-cooperative game combined with different versions of the ant colony algorithm for the VM placement. The main goal is to achieve load balancing by placing the VMs on the PMs based on the PM’s current state. In [29], the non-cooperative game has been used to minimize the cost of operating a DC. Besides having the operational cost reduced, the proposed scheme achieves fairness, and better average response time for all the client regions as compared to the existing schemes (PROP, GOS).
In [30], the Stackelberg game between the monitor and the schedulers has been used to model the problem. The goal is to minimize energy consumption and average response time. The model outperforms NPA, DVFS, and DCP schemes. In [31], using evolutionary game theory among the VMs, the authors proposed a solution to optimize the power consumption. It minimizes the energy consumption by switching off the unused physical machines. It performs better as compared to the FF
(First Fit), the BFI (Best Fit Increasing), the BFD (Best Fit Decreasing), the Greedy, and the Load Balance (LB). How-ever, if switching the PMs between on and off is too frequent, it will result in more power consumption and performance degradation.
Researchers have shown great interest in solving the re-source allocation problem in large-scale DC using the GT. The resource allocation process is an optimization problem. In the literature, however, modeling of the DC scheduling as an optimization problem appears to be an understudied topic. Moreover, the existing studies do not consider the ambient effect of the surrounding nodes while assigning the user jobs. Therefore, in this paper, we focus on reducing the thermal imbalances within the DC environment by investigating the cooperative game theory and present a TA resource allocation algorithm to optimize the thermal balance in the DC envi-ronment. The proposed strategy considers the effect of jobs running on the surrounding nodes which helps in reducing the number of migrations while still achieving better thermal uniformity.
III. DATACENTERMODEL
The proposed scheduling scheme follows the DC archi-tecture presented in [32], where the high-level centralized controller (HLCC) manages and allocates the incoming jobs based on the thermal profiles of the computing nodes. In GTARA, however, the HLCC allocates jobs based on the thermal profile of both the computing nodes and the incoming jobs. The HLCC assigns the hottest job to the coolest low-level centralized controller (LLCC), as shown in Fig. 1. The LLCC, after receiving jobs from the HLCC, allocates the job to the appropriate server based upon their temperatures and the ambient effect of the surrounding nodes. Green color indicates the coolest while red color indicates the hottest pod/server. The servers and the LLCCs are organized into pods in such a way that each pod has one LLCC. The LLCC controls all the servers contained in its corresponding pod. Whenever a server is overheated (i.e. its temperature exceeds the threshold
temperatureTÛ), the LLCC migrates some of its tasks to other
servers. The migration is either intra-pod (within the same pod) or inter-pod (to some other pod). The intra-pod migration is preferred over the inter-pod migration whenever feasible; else, the inter-pod migration is considered. The migration of tasks from one pod to the other is through the HLCC. The LLCC requests HLCC to migrate a task to some other pod. Before going into the discussion of the proposed cooperative game, in the next section, we will briefly present the thermodynamics of the DC environment.
A. Thermodynamics
In this section, we present a brief description of the heat dissipation due to the computing nodes and its effect on the surrounding nodes. A complete model and analysis of the thermodynamics in the DC is provided in [33]. The energy consumption of a computing node depends on hardware characteristics, and nature of the jobs assigned. The energy consumed by a computing node is directly converted to heat
Fig. 1: Allocation of jobs: the HLCC assigns job to the coolest LLCC; the LLCC allocates the job to the coolest
server.
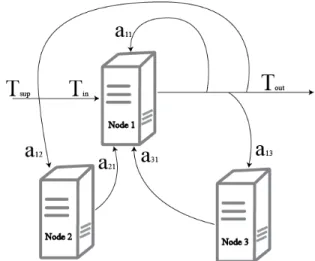
energy and is dissipated into the DC environment, which raises the temperature of surrounding nodes. This situation is also referred to as ambient temperature in the literature. Fig. 2 illustrates the phenomena of the ambient effect in the DC environment, where every computing node has an
input temperature denoted by Tin and an output temperature
denoted byTout. As shown in Fig. 2,Tin of Node 1 involves
the ambient temperature due to surrounding nodes and the
supplied cooling temperature (Tsup) from CRAC (Computer
Room Air Conditioning) units. According to [32], the effect of one node on its surrounding nodes inside the DC environment can be represented by a cross coefficient matrix as follows:
a11 a12 a13
|a21 a22 a23| a31 a32 a33
(1)
In the above matrix,aij is the heat recirculation from server i
to server j and is given by:
aij=Tiout∗Υ∗1/νj, (2)
whereΥ represents the constant of thermal conductivity, and
νj is the number of hops from node j to node i.
LetΛbe the amount of heat carried by the airflow per unit
time and is given by:
Λ=p f CT, (3)
where p denotes air density, f represents the rate of airflow, C denotes the specific heat of air, and T is the air temperature.
The amount of outlet heat Λiout for any node in the DC is
given by:
Λiout=Λiin+Pi, (4)
where Pi is the power consumed by the node i and Λiin
denotes the inlet heat of nodei. It can be calculated as:
Λiin = n
Õ
j=1
(ajiΛjout)+Λisup. (5)
Fig. 2: Heat recirculation inside DCs
Using the above equation, we can calculate the ambient effect
of the surrounding nodes. Hence, substituting the value ofΛiin,
Eq. (4) becomes: Λiout= n Õ j=1 (ajiΛjout)+Λisup+Pi, (6)
which can also be written as:
Λiout= n Õ j=1 (ajip f CTjout)+Λisup+Pi. (7) B. Proposed CG
Definition:A CG [34] comprises the following: i. N={1, ...,n} agents/players indexed byi.
ii. χ⊆ <Ndefines the set of actions/strategies fornagents,
which is non-empty, closed and convex.
iii. For each playeri, ficalculates the utility. fi specifies the
mapping χ 7→ <and is bounded above. The objective
is to maximize fi(<) for every agent i where < is the
strategy followed by the agent i.
iv. For each player i, ρoi is the minimum value of fi that
each player i expects from the system. The agents will
keep cooperating as long as the system provides the
minimum payoffρoi. Hence, there is an initial agreement
point denoted by the vector ρo ={ρo1, ρo2, ..., ρon}.
Mapping (Proposed CG): In the TA resource allocation inside the DC:
i. HLCC andn−1LLCCs are the players in our proposed
CG, where HLCC works as a broker and controls the distribution of jobs among LLCCs in a fair and stable way. By fair and stable, we mean that during allocating of jobs, HLCC selects LLCCs in a way in which the jobs are allocated based on thermal signature. LLCC then assigns the job to an appropriate server. As soon as the job is allocated, the thermal signature of that server increases so as the average thermal signature of the pod. As a result, the next job will be assigned to a different pod having thermal signature less than the previous pod.
In the same way, all jobs will be allocated fairly to all pods, while keeping the thermal status of the DC balanced. Moreover, to keep the temperature uniform, migrations are also performed if the threshold value of the server is about to be exceeded.
ii. The set of possible strategies for HLCC contains all LLCCs while the set of possible strategies for LLCC comprises all the servers contained in the corresponding pod. The parameters that affect decision making while selecting an appropriate strategy (LLCC or server) in-clude (1) the thermal profile of the computing nodes, (2) the temperature rise due to running a job and (3) the ambient effect of surrounding nodes.
iii. The function fi(<) calculates the utility (payoff) for
each player when it selects a particular strategy <
(LLCC/server) while distributing the incoming jobs and is given by: fi(<)=TÛ/T(<)+g(<), (8) where g(x)= ( 1,i f T(<)+∆T+∆(T(<))in<TÛ 0,ot herwise (9)
whereT(<) is the temperature of the computing node
selected by the playerito run the job.∆T represents the
temperature rise due to running the job, and∆(T(<))inis
the change in ambient effect of the surrounding nodes. The ambient effect can be calculated using Eq. (5).
iv. The minimum utility/payoff (ρo) that each LLCC
ex-pects from the cooperation is 1, which is obtained when
the temperature of computing node equalsTÛ.
Definition (Achievable performances): Let % ⊆ <N de-fines non-empty set of all feasible performances that can
be achieved by players in the CG. Let % is non-empty
and bounded below. Let ψ = {υ ∈ U|υ ≥ ρo} defines
achievable performances set with reference to ρo. So a CG
can be formally written as G= {(%, ρo)|% ⊂ <N and ρo ⊂
<N|ψ is non−empty}.
Definition (Pareto Optimality): Let us suppose that f(<)=
f1(<), ., fn(<), wher e < ∈ χ and f(<) ∈ %. The < is Pareto
Optimal (PO) if∀<∈ χ, fi( Û<) ≥ fi(<)imply fi( Û<)= fi(<), i∈
{1, ....,n}.
Now, we are going to find the PO solutions for the proposed
game we have just defined. According to [35], for the n
-players CG, the set of PO points construct ann−1dimensional
hyperspace populated by infinite points. To find the optimal point, we consider some fairness axioms that specify the Nash Bargaining Solution (NBS) [36]. Hence, the NBS can provide better resource allocation scheme that is fair and stable.
Definition (NBS):A mapping ς:G→ <N is a NBS if i. ς(%, ρo) ∈ψ.
ii. ς(%, ρo) satisfies pareto-optimality if the following
ax-ioms are satisfied:
iii. Linearity Axioms: φ : <N → <N,wher e φ(ρoi) =
aiρi +bi,ai > 0, i ∈ {1, ....,n} t hen ς(φ(%), φ(ρo)) =
φ(ς(%, ρo)).
iv Irrelevant Alternatives Axioms: If % ⊂ %, ςÛ ( Û%, ρo) ∈ %, t hen ς(%, ρo)=ς( Û%, ρo).
v Symmetry Axiom:Two players will get the same utility if
they have same ρo
i (initial performance) and same fi(<).
In brief, Axiom III states that affine scaling of the per-formance function does not change the NBS; Axiom IV says enlarging the domain does not affect the bargaining point; and according to Axiom V, players will have the same performances if they have the same initial points and the objective functions.
Definition: (Bargaining Point.) ifρ*is specified byς(%, ρo),
then ρ* is a bargaining point.
C. Theorem (Nash Bargaining Point Specification):
Let χÜ be the compact subset of <N and is convex. Let
fi : χÜ → <, i ∈ {1, ...,n} be the concave function and
bounded above. Let f(<)=(f1(<),f2(<), ...,fn(<)), %={ρ|ρ∈
<N}}, and χÜ
o ={<∈ Üχ|f(<) ≥ ρo} be the actions set that
allows players to get payoff which is at least equal to the minimum performance they expect. Then:
i. There exists a unique ρ∗ which is a bargaining solution.
ii. f-1(ρ∗), the set of bargaining solutions, can be found
as follows: Let K denotes a set of players that can
achieve performance strictly greater then their initial per-formances, that isK={κ|κ ∈1,2, ...,n|∃ <∈ χ0,fj(<)>
ρo
κ}.Every vector <∈ f−1(ρ∗)veri f ies fκ(<)> ρoκ for
every κ∈K and solves the optimization problem:
maxÖ
κJ
(fκ(<) −ρoκ),<∈ χo.
Therefore,ρ*satisfiesρ∗κ ≥ρoκ andρ∗κ =ρ0κot herwise.
IV. PROPOSEDSCHEDULINGSCHEME
Let P denotes a set of all the pods in the DC indexed by
i andT P be the list containing temperatures of all the
corre-sponding pods in P. Therefore,T P(i) means the temperature
ofith pod inP. Byith pod we meanith LLCC since each pod
has a single LLCC associated with it. Letargmax[T P(i)]and
argmin[T P(i)]be the two functions defined overT Pthat finds the temperature of the hottest and the coolest pod respectively. Mathematically, the functions can be written as:
argmax(T P(i))={T P(i)|T P(i) ≥T P(j),∀i,j∈T P} (10)
argmin(T P(i))={T P(i)|T P(i) ≤T P(j),∀i,j∈T P} (11) The overall objective of proposed CG is to optimize the following function:
minimize[argmax[T P(i)] −argmin[T P(i)]] (12) subject to,
TVji+∆T +∆(TVji)in <TÛ,
where TVji denotes the temperature of individual server V
in the ith pod indexed by j., ∆T represents the temperature
rise due to running a job, ∆(TVji)in is the change in ambient
effect of surrounding nodes, and TÛ denotes the threshold
temperature of the computing node. According to Eq. (10), if the temperature difference between the hottest and coolest pod is minimized, there will be uniform temperature in all areas inside the DC environment. To minimize the thermal
difference among the pods, we propose a three step game based on the following decision variables: (1) thermal profile of a computing node, (2) temperature rise due to running a job, and (3) the ambient effect of the surrounding nodes. Following are the steps in our CG to achieve the aforementioned objectives:
A. Step 1: Assigning job to LLCC
When new jobs arrive, the HLCC sorts them in descending order of their temperatures (i-e hottest jobs are served first). Assigning the hottest jobs to the coolest computing nodes results in the lower temperature values of the computing nodes. The HLCC finds the coolest LLCC (pod) and assigns the hottest job to it. By doing so, we are actually trying to lower the temperature difference between the hottest and coolest pod as described by the Eq. 12. When a job is assigned to the LLCC, the next step is to find the appropriate server to run that job.
B. Step 2: Assigning the job to an appropriate server
In order to keep the temperature of a server under the threshold temperature and avoid hotspot, we need to find an appropriate server. the LLCC first sorts the servers in ascending order of their temperatures. After sorting, the LLCC calculates the utility of assigning the job to a server using Eq. (6), where <denotes a server within thepod(i). Since the objective is to maximize the utility function fi(<)−ρo, a server
that results in maximum utility fi(<)is selected.
C. Step 3: When a server reaches the threshold temperature
When a server reaches its threshold temperature TÛ,
migra-tion of some tasks is considered from the server to some other server(s) in the same pod if feasible. If migration within the same pod is not suitable, then the LLCC requests the HLCC for inter-pod migrations. The LLCC prefers job migrations within the same pod but before doing so, it needs to check if the assignment results in any hotspots by using the same utility function as in step 2. If it is not feasible to assign jobs to any of the servers within the same pod, then the LLCC hands over the job to the HLCC. The HLCC will assign the job to any other LLCC whose temperature is the lowest of all the LLCCs.
Fig. 3: Short/Long Jobs Percentage
Fig. 4: Jobs distribution in percentage with respect to number of CPUs
V. FINDINGS
To evaluate the GTARA, simulations are carried out in a simulation tool [33] using a real DC workload taken from the ”Center of Computational Research (CCR), State University New York at Buffalo, Buffalo, NY, USA”. The GTARA is benchmarked against the FCFS (First-Come First-Served), the TACS (Thermal-aware Control Strategy) [32], and the TASA (Thermal-aware Scheduling Algorithm) [25]. The dataset used in the simulation contains 22385 jobs (each job having multi-ple tasks) recorded over a period of one month: from 20 Feb 2009 to 22 mar 2009. The jobs are distinguished as either short having lenghth less than 1hour or long having length greater than 1 hour. There are 10,428 jobs that are short and 11,957 jobs that are long as shown in Fig. 3. The percentage of jobs with respect to the number of CPUs used is shown in Fig. 4. The jobs were executed on 1056 servers arranged in 33 racks. The servers have dual-core processors with a speed of 3.0/3.2 GHz.
Before going into the discussion of simulation results, let us first look at how each scheduling scheme works. The FCFS allocates jobs based on the order of their arrival time. The TACS assigns jobs to the computing nodes if the temperature rise due to the job does not cross the threshold temperature. When a server reaches its threshold temperature, it migrates the jobs running on the server to some other server(s).
Sim-Fig. 5: Number of hotspots and migrations: A comparative summary.
20 30 40 50 60 70 80 90 100
1.235059E+09 1.236259E+09 1.237459E+09
Epoch Time Tem peratu re Dif fere nc e (⁰F) (a) FCFS 20 30 40 50 60 70 80 90 100
1.235059E+09 1.236259E+09 1.237459E+09
Epoch Time Tem peratu re Dif fere nc e (⁰F) (b) TACS 20 30 40 50 60 70 80 90 100
1.235059E+09 1.236259E+09 1.237459E+09
Epoch Time Tem peratu re Dif fere nc e (⁰F) (c) TASA 20 30 40 50 60 70 80 90 100
1.235059E+09 1.236259E+09 1.237459E+09
Epoch Time Tem peratu re Dif fere nc e (⁰F) (d) GTARA
Fig. 6: Temperature differences between the hottest pod and coolest pod.
ilarly, the TASA allocates jobs based on the thermal profile of the computing nodes and the temperature of incoming jobs. However, the TASA does not take any remedial action when a server reaches its threshold temperature. The main difference between the GTARA and its competitors is that they do not consider the ambient effect of the surrounding nodes at the time of job allocation. Moreover, the GTARA optimizes the resource scheduling process by choosing the best choice among available solutions. The parameters that affect the decision making while allocating resources include (1) the thermal profile of the computing nodes, (2) the temperature rise of a job and (3) the ambient effect of the surrounding nodes.
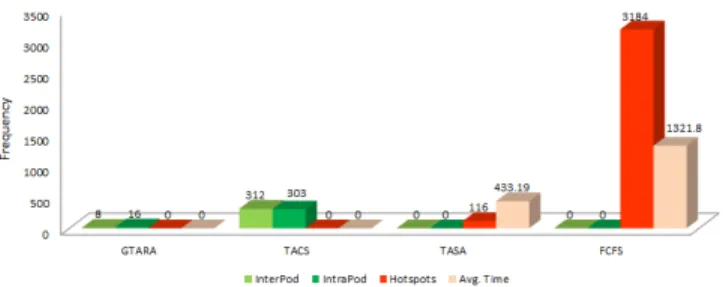
Fig. 5 shows the number of hotspots and migrations against each job scheduling algorithm. It is observed that the FCFS results in a huge number of hotspots: the number of hotspots is 3184 and the lifetime of each hotspot is very long (i-e 1321 seconds on average). However, in the case of TASA, the number of hotspots is significantly reduced (to 116) and the lifetime of a hotspot is much shorter (i-e around 433 seconds) as compared to the FCFS, due to the allocation of incoming jobs based on the thermal profile of the computing nodes. In the case of TACS and GTARA, hotspots are avoided at the cost of the interpod/intrapod migrations. However, it is observed that the GTARA results in fewer number of migrations: the number of interpod and intrapod migrations in the TACS is 312 and 303, respectively, whilst in GTARA, the numbers are respectively reduced to 8 and 16. The consideration of
the ambient effect of the surrounding nodes prior to the job assignment helps the GTARA avoid hotspots and migrations (interpod/intrapod).
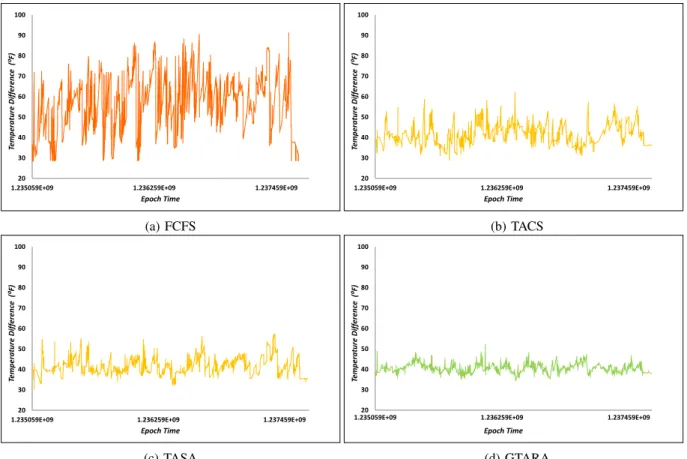
Fig. 6 depicts the temperature differences between the hottest and coolest pods with respect to time for each schedul-ing scheme. The x-axis and y-axis represent the epoch time and temperature difference in °F, respectively. Fig 3(a), Fig 3(b), Fig. 3(c), and Fig 3(d) plot the temperature differences for the FCFS, TACS, TASA, and GTARA strategies respec-tively. The greater the temperature difference, the higher the thermal imbalance within the DC. It can be observed that the FCFS, TACS, and TASA result in higher temperature differences as compared to the GTARA. The temperature difference for the FCFS is most of the time between 45°F and 60°F, while in some cases it reaches 80°F. Compared to FCFS, both the TASA and the TACS achieve much better thermal uniformity, but they result in sudden peak values more frequently (i.e. presence of hotspots), which results in more migrations (in the case of TACS). The temperature difference for the TASA and the TACS range from 35°F to 45°F for most cases. However, in some situations, they reach 55°F. The GTARA avoids scenarios where such a high thermal imbalance may arise by considering the thermal profile of both the jobs and the computing nodes. The temperature difference for GTARA is in most cases the same as the TASA and the TACS (i-e between 35°F and 45°F). However, in some cases, the temperature difference is even smaller than that and it also avoids sudden peak values where hotspots may
arise. Overall, the GTARA results in a negligible number of migrations while still achieving better thermal uniformity inside the DC environment.
VI. CONCLUSION
In this research, we proposed a Game-based Thermal-Aware Resource Allocation (GTARA) strategy, which is designed to minimize thermal imbalance and avoid hotspots within the DC. In the strategy, the cooperative game among HLCC and LLCCs is designed to optimize the thermal-aware resource allocation process to achieve better thermal balance while keeping the number of migrations to a minimum.
Evaluations using real-world DC workload demonstrated that the GTARA outperforms other similar approaches, in terms of thermal balance (by assigning the hottest jobs to the coolest computing nodes) and avoiding hotspots with fewer number of inter-pod/intra-pod migrations (by calculating the ambient effect of the surrounding servers prior to assigning job to any particular server and, then, selecting the best choice among all the servers).
In the future, we will consider the heterogeneity of comput-ing nodes, and analyze the effect of the proposed strategy on the response time of incoming jobs as well as the satisfaction rate of those jobs.
REFERENCES
[1] James Hamilton. Cooperative Expendable Micro-Slice
Servers (CEMS): Low Cost, Low Power Servers for Internet-Scale Services. 2009.
[2] Richard E Brown et al. Report to congress on server
and data center energy efficiency: Public law 109-431. Tech. rep. Ernest Orlando Lawrence Berkeley National Laboratory, Berkeley, CA (US), 2007.
[3] Muhammad Tayyab Chaudhry et al. “Thermal-Aware
Scheduling in Green Data Centers”. In:ACM Comput.
Surv. 47.3 (Feb. 2015), 39:1–39:48. ISSN: 0360-0300.
DOI: 10 . 1145 / 2678278. URL: http : / / doi . acm . org / 10 . 1145/2678278.
[4] Luca Parolini et al. “A cyber–physical systems approach
to data center modeling and control for energy
effi-ciency”. In: Proceedings of the IEEE 100.1 (2012),
pp. 254–268.
[5] Linlin Wu, Saurabh Kumar Garg, and Rajkumar Buyya.
“SLA-based admission control for a Software-as-a-Service provider in Cloud computing environments”. In:
Journal of Computer and System Sciences78.5 (2012), pp. 1280–1299.
[6] Anton Beloglazov, Jemal Abawajy, and Rajkumar
Buyya. “Energy-aware resource allocation heuristics for efficient management of data centers for Cloud
com-puting”. In: Future Generation Computer Systems28.5
(2012). Special Section: Energy efficiency in large-scale
distributed systems, pp. 755 –768. ISSN: 0167-739X.
DOI: https : / / doi . org / 10 . 1016 / j . future . 2011 . 04 . 017.
URL: http://www.sciencedirect.com/science/article/pii/
S0167739X11000689.
[7] A. Shehabi et. al. United States Data Center Energy
Usage Report. Tech. rep. EE Office of Federal Energy Management (EE-2L). 2016.
[8] Tobias Van Damme, Claudio De Persis, and Pietro Tesi.
“Optimized Thermal-Aware Job Scheduling and Control
of Data Centers”. In:arXiv preprint arXiv:1611.00522
(2016).
[9] Muhammad Zakarya and Lee Gillam. “Energy efficient
computing, clusters, grids and clouds: A taxonomy and
survey”. In: Sustainable Computing: Informatics and
Systems14 (2017), pp. 13–33.
[10] Jiachen Yang et al. “A task scheduling algorithm
con-sidering game theory designed for energy management
in cloud computing”. In: Future Generation Computer
Systems(2017).
[11] Kashif Bilal et al. “Trends and challenges in cloud
datacenters”. In: IEEE Cloud Computing 1.1 (2014),
pp. 10–20.
[12] Qinghui Tang, Sandeep KS Gupta, and Georgios
Varsamopoulos. “Thermal-aware task scheduling for data centers through minimizing heat recirculation”. In:
Cluster Computing, 2007 IEEE International Confer-ence on. IEEE. 2007, pp. 129–138.
[13] Justin Moore, Jeffrey S Chase, and Parthasarathy
Ran-ganathan. “Weatherman: Automated, online and predic-tive thermal mapping and management for data
cen-ters”. In:Autonomic Computing, 2006. ICAC’06. IEEE
International Conference on. IEEE. 2006, pp. 155–164.
[14] Justin D Moore et al. “Making Scheduling" Cool":
Temperature-Aware Workload Placement in Data
Cen-ters.” In:USENIX annual technical conference, General
Track. 2005, pp. 61–75.
[15] Qinghui Tang et al. “Thermal-aware task scheduling
to minimize energy usage of blade server based
data-centers”. In:Dependable, Autonomic and Secure
Com-puting, 2nd IEEE International Symposium on. IEEE. 2006, pp. 195–202.
[16] Andreas Merkel, Jan Stoess, and Frank Bellosa.
“Resource-conscious scheduling for energy efficiency
on multicore processors”. In:Proceedings of the 5th
Eu-ropean conference on Computer systems. ACM. 2010, pp. 153–166.
[17] Jeonghwan Choi et al. “Thermal-aware task scheduling
at the system software level”. In: Proceedings of the
2007 international symposium on Low power electron-ics and design. ACM. 2007, pp. 213–218.
[18] Adam Lewis and Nian-Feng Tzeng. “Thermal-Aware
Scheduling in Multicore Systems Using Chaotic Attrac-tor PredicAttrac-tors”. In: ().
[19] Lizhe Wang, Samee U. Khan, and Jai Dayal. “Thermal
aware workload placement with task-temperature
pro-files in a data center”. In:The Journal of
Supercomput-ing 61.3 (2012), pp. 780–803. ISSN: 1573-0484. DOI:
10.1007/s11227- 011- 0635- z. URL: https://doi.org/10.
1007/s11227-011-0635-z.
[20] Violaine Villebonnet and Georges Da Costa.
In: WETICE Conference (WETICE), 2014 IEEE 23rd International. IEEE. 2014, pp. 115–120.
[21] Jing V Wang, Chi-Tsun Cheng, and K Tse Chi. “A
power and thermal-aware virtual machine allocation
mechanism for Cloud data centers”. In:Communication
Workshop (ICCW), 2015 IEEE International Confer-ence on. IEEE. 2015, pp. 2850–2855.
[22] Mengxuan Song et al. “Thermal-aware load balancing
in a server rack”. In:Control Applications (CCA), 2016
IEEE Conference on. IEEE. 2016, pp. 462–467.
[23] Qiu Fang et al. “Thermal-aware Energy Management
of HPC Data Center Via Two-time-scale Control”. In:
IEEE Transactions on Industrial Informatics (2017).
[24] Eun Kyung Lee, Hariharasudhan Viswanathan, and
Dario Pompili. “Proactive thermal-aware resource man-agement in virtualized HPC cloud datacenters”. In:
IEEE Transactions on Cloud Computing (2017).
[25] Lizhe Wang et al. “Towards thermal aware workload
scheduling in a data center”. In: Pervasive Systems,
Algorithms, and Networks (ISPAN), 2009 10th Interna-tional Symposium on. IEEE. 2009, pp. 116–122.
[26] Zhigang Jiang et al. “Thermal-aware task placement
with dynamic thermal model in an established
data-center”. In: Innovative Mobile and Internet Services
in Ubiquitous Computing (IMIS), 2014 Eighth Interna-tional Conference on. IEEE. 2014, pp. 1–8.
[27] Hadi Khani et al. “Distributed consolidation of virtual
machines for power efficiency in heterogeneous cloud
data centers”. In: Computers & Electrical Engineering
47 (2015), pp. 173–185.
[28] Khiet Thanh Bui, Tran Vu Pham, and Hung Cong Tran.
“A Load Balancing Game Approach for VM Provision Cloud Computing Based on Ant Colony Optimization”. In:International Conference on Context-Aware Systems and Applications. Springer. 2016, pp. 52–63.
[29] Rakesh Tripathi et al. “Non-cooperative power and
la-tency aware load balancing in distributed data centers”. In:Journal of Parallel and Distributed Computing107 (2017), pp. 76–86.
[30] Bo Yang et al. “Stackelberg game approach for
energy-aware resource allocation in data centers”. In: IEEE
Transactions on Parallel and Distributed Systems27.12 (2016), pp. 3646–3658.
[31] Zhijiao Xiao et al. “A solution of dynamic VMs
place-ment problem for energy consumption optimization
based on evolutionary game theory”. In: Journal of
Systems and Software101 (2015), pp. 260–272.
[32] Saif UR Malik et al. “Modeling and analysis of the
ther-mal properties exhibited by cyberphysical data centers”. In:IEEE Systems Journal 11.1 (2017), pp. 163–172.
[33] Rahmat Ullah et al. “Simulator for Modeling, Analysis,
and Visualizations of Thermal status in Data Centers”. In: Sustainable Computing: Informatics and Systems
(2018).
[34] Alvin E Roth. Axiomatic models of bargaining.
Vol. 170. Springer Science & Business Media, 2012.
[35] Christos H Papadimitriou and Mihalis Yannakakis. “On
the approximability of trade-offs and optimal access of
web sources”. In: Foundations of Computer Science,
2000. Proceedings. 41st Annual Symposium on. IEEE. 2000, pp. 86–92.
[36] John C Harsanyi. “A simplified bargaining model for
the n-person cooperative game”. In:International
Eco-nomic Review4.2 (1963), pp. 194–220.
Saeed AkbarSaeed Akbar completed his MS(SE) from COMSATS University, Islamabad. Currently, he is a lecturer at Department of Computer Science, IQRA National University, Peshawar Pakistan. His research interest includes routing algorithms in dis-tributed systems, algorithmic game theory, and high performance computing systems.
Saif U. R. Malik Dr. Saif U. R. Malik did his Ph.D. from North Dakota State University, USA. He worked as an Assistant Professor at COMSATS Uni-versity, Islamabad Pakistan since 2014. Currently, he is a Senior Researcher at Cybernetica, AS Estonia. His areas of expertise include the application of Formal Methods in Large Scale Computing Systems, Distributed Computing, Data Centres, and Routing Protocols.
Kim-Kwang Raymond Choo (SM’15) received the Ph.D. in Information Security in 2006 from Queensland University of Technology, Australia. He currently holds the Cloud Technology Endowed Professorship at The University of Texas at San Antonio (UTSA), and has a courtesy appointment at the University of South Australia. In 2016, he was named the Cybersecurity Educator of the Year - APAC (Cybersecurity Excellence Awards are pro-duced in cooperation with the Information Security Community on LinkedIn), and in 2015 he and his team won the Digital Forensics Research Challenge organized by Germany’s University of Erlangen-Nuremberg. He is the recipient of the 2018 UTSA College of Business Col. Jean Piccione and Lt. Col. Philip Piccione Endowed Research Award for Tenured Faculty, IEEE TrustCom 2018 Best Paper Award, ESORICS 2015 Best Research Paper Award, 2014 Highly Commended Award by the Australia New Zealand Policing Advisory Agency, Fulbright Scholarship in 2009, 2008 Australia Day Achievement Medallion, and British Computer Society’s Wilkes Award in 2008. He is also a Fellow of the Australian Computer Society, an IEEE Senior Member, and Co-Chair of IEEE Multimedia Communications Technical Committee (MMTC)â ˘A ´Zs Digital Rights Management for Multimedia Interest Group.
Samee U. KhanSamee U. Khan received a PhD in 2007 from the University of Texas, Arlington, TX, USA. Currently, he is the Lead Program Director (Cluster Lead) for the Computer Systems Research at the National Science Foundation. He also is a faculty at the North Dakota State University, Fargo, ND, USA. His research interests include optimiza-tion, robustness, and security of computer systems. His work has appeared in over 400 publications. He is on the editorial boards of leading journals, such as ACM Computing Surveys, IEEE Access, IEEE Communications Surveys and Tutorials, IET Wireless Sensor Systems, IET Cyber-Physical Systems, and IEEE IT Pro. He is an ACM Distinguished Speaker, an IEEE Distinguished Lecturer, a Fellow of the Institution of Engineering and Technology (IET, formerly IEE), and a Fellow of the British Computer Society (BCS). The work of Samee U. Khan was supported by (while serving at) the National Science Foundation. Any opinion, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.
Naveed Ahmad Dr. Naveed Ahmad received his Ph.D., in engineernig design from University of Cambridge, U.K. Currently, he is serving as an Assistant Professor in COMSATS University, Islam-abad Pakistan. His research interests include change management, process management, and software de-velopment.
Adeel Anjum Dr. Adeel Anjum is an Assistant Professor in the department of Computer Sciences at COMSATS University Islamabad Campus. He completed his Ph. D., with distinction in the year 2013. His area of research is data privacy using artificial intelligence techniques.