Nonlinear Vibration of Isotropic Thick Rectangular Mindlin Plate with Different Boundary Condition

(1)

International Journal of Emerging Technology and Advanced Engineering

Website: www.ijetae.com (ISSN 2250-2459, UGC Approved List of Recommended Journal, Volume 7, Issue 11, November 2017)

468

Nonlinear Vibration of Isotropic Thick Rectangular

Mindlin Plate with Different Boundary Condition

Ankit Dasgupta1, Atanu Dutta2

1,2_{M.Tech Students, School of Civil Engineering. KIIT University, Bhubaneswar, Odisha, India}

Abstract: In recent years, there are many plate bending elements that emerged for solving both thin and thick plates. Plates on elastic foundation have wide application in structural engineering such as rough foundation, storage tanks, swimming pools etc. The main features of these elements are based on mixed formulation interpolation with discrete collocation constraints. The focus of the present study is only on free vibration of rectangular thick plate with an edge free and the formulation based on the Reissner-Mindlin plate theory, considering the first odder shear deformation effect taking into account of rotary inertia. The plate structure problems have been different combinations of boundary condition to determine the nonlinear natural frequency, mode shapes of plate. The static problem corresponding to a uniform transverse loading is solved first and the dynamic problem is subsequently taken up with the unknown deflection field. The Hamiltonian system based governing equation is first constructed. The eigenvalue problems of two fundamental vibrations are formed for a thick plate with an edge free and the others clamped. The present results for frequency parameter and the numerical model are in corporate after performing the test of convergence and experimental significance, validation has been done for large vibration around the fundamental resonance of the steel plate are tested and 3D mode shape are also plotted to show the deflected shape of the plates.

Key words: Isotropic thick plate, Shear deformation theory, finite element method, Mixed formulation, 3D mode shape, nonlinear frequency.

I. INTRODUCTION

In recent days, plate structures have established lot of interest by diversified and potential application in automobile and aerospace industry due to their strength capabilities. Plate structure play an important role in engineering application such as the bridge decks, storage tanks, foundation beds, aircraft panel etc. In solid mechanics, the plates are normally categories according to the ratio of thickness to the in-plane dimension and mechanical properties such as laminated composite plate, Mindlin-Reissner plate, functionally graded material plate (FGM) etc. Laminated composite plate is a combination of different type of composite and matrix materials and functionally graded material plate is made of a metal and ceramic [23,21]. In this paper we are considering isotropic thick rectangular Mindlin plate. During the last decade, a number of researchers applied dependability techniques to this isotropic thick plate. Ribeiro et al. [22] is trying to investigate the difference between oscillations of regular composite laminate plate and traditional laminate by using Newmark’s method. Talha et al. [16] using rectangular FGM plate and higher order shear deformation theory to find out the modification of transverse displacement in conjunction with finite element method (FEM). Among the large number of plate bending elements developed in recent years is a set of triangular and quadrilateral finite elements that were introduced by Zienkiewicz et al. [20] and Taylor

(2)

469

Senjanovic et al. [10] noted that the Mindlin theory operate with bending deflection as the basic variable for the total (bending + shear) deflection and the angle of rotation and also determined the formulation of eigenvalue problem and natural frequency. Wang et al. [3] the major difference between both plate theories are that the Ressiner plate theory was derived from the variation principle of the complimentary strain energy with linear bending stress distribution and on the other hand Mindlin formulated [4] the finite deference technique to calculate frequencies of rectangular plate with linear varying thickness. By making the formulation[9] of the problem and the fundamental solutions are satisfy with the boundary conditions of the original plate, the equation with respect to the natural frequency is obtained and the mode shape solutions corresponding to the natural frequencies has been formed. Comprehensive numerical results, including both the natural frequencies and associate mode shapes are listed to demonstrate the convergence and accuracy of the new analytic solution by satisfactory agreement with those formed the finite element analysis (FEA)

.

II. FUNDAMENTAL FREE VIBRATION PROBLEM

It is more difficult to obtain the exact solutions for the free vibrations of rectangular plate compared with thin plate, due to the increase of the number of governing equations and independent coordinates. For this reason many determinations were dedicated to develop approximate solutions with a maximum level of accuracy based on Mindlin plate theory (MPT). FEM, finite strip method, spline strip method, Rayleigh-Ritz method and collocation methods have been widely used to study the free vibrations of Mindlin rectangular plate. Liew et al.[18,26 ] have presented a wide-ranging literature survey on the research works up to 1994 on vibrations of thick plates. Shen et al [25] concluded that Dynamic response was determined by using both the modal superposition approach (MSA) and state variable approach (SVA). Many publications have appeared in the literature on the free of isotropic thick plates. At present study is associated with free vibration of isotropic thick rectangular Mindlin plate with various type of boundary condition by using finite element formulation and we have also discuss, a few existing work related to this computational procedure. The proposed theories exactly satisfy the transverse stress boundary condition on the bottom and top surface of the plate and the new results for the Eigen frequencies with different combination of classical boundary condition are incorporated after performing a convergence study and validation in special cases available in the literature. The effect of variations in the some material and geometric properties of the plate, we have been studied. Let us considered an isotropic thick rectangular plate of length (in x direction), breadth (in y direction) and uniform thickness as a, b and h respectively.

The fundamental study in the analysis of large amplitude vibration of rectangular plates is due to analytical study of free vibration [14, 24].

III. FUNDAMENTAL BOUNDARY CONDITION

In the contemporary investigation, non-linear free vibration analysis is done for isotropic thick plate and the coordination of the plates with its unreformed middle surface of the Cartesian co-ordinate system with its origin at “O” (x, y, z).[2] All the shear deformation theories are considered with the physical parameters like length to breadth ratio (b/a) (1, 2, 3, 4, 5) and thickness to length ratio (h/a) (0.1. 0.05, 0.01) respectively. The various boundary conditions have been considered. Four boundary conditions are considered and results are compared: (i) simply supported plate with immovable edges, (ii) all edges are clamped, (iii) two opposite edges clamped and simply supported and (iv) one edges are free and others edges are clamped. As shown in the figure, the thick rectangular plate with an edge free (denoted by “F”), simply supported (denoted by “S”) and clamped (denoted by “C”). now we considered “CCCC” , “SSSS”, “CSCS” and “CCCF” plates, where the four letters symbolic notation is used in anticlockwise direction.

IV. FORMULATION

A. Equilibrium equations

The equations of motion for free un-damped vibration of an elastic system undergoing large displacement can be expressed in the following matrix form,

 

K

 

 

 

M

 

 

 

0

In which _{ }K and

 

M are overall stiffness and mass

matrices and

 

_ is the displacement vector.

B. Shape functions

If displacements at a node

r

of a quadratic isoparametric element are

_{u v w}

_{r r}

,

_r

,



_xr

and



_yr

,

then at any point inside the element In which,



_ris the shape function at a

node

r

 



u v w



x y

    

 



u v w



r r r r xr yr

   

C. Linear and Non-Linear Stiffness Matrices

The plate strains are describes in term of middle surface displacements i. e. x-y plane coincides with the middle surface.

(3)

470

Where

 

2 2 2 2 2 2 u x v y u v y x w x L w y w x y x y        _        _        _      _ _       _   _            _   _     _         _     _      And





2 1 2 2 1 2 0 0 0 0 0 w x w y w w x y NL   __ _   _ _              _       __ ___ _  _ _ _ _ _{ } _ _                  

In which the first term is the linear expression and the second term gives non-linear terms. If linear elastic behavior is considered, the stress-strain relationship is written as

 

B B B

L  NL  

     

     

In which B L

 

 , is the same matrix as in linear infinitesimal strain analysis, only _B

NL

 

  depends on the displacement. In general, _B

NL

 

 is found to be a linear function of such displacement. Therefore,

 





 

d d d B B d

L NL L NL

 _  _  _  _      

Which, because d

 

 is arbitrary, gives the equilibrium equation as

  

   

0

T

B D dv R

v



   

  





 

1

 

   

0 2

T

B B D B B dv R

L NL L NL

v         _  _ _ _  _ _ _ _ _ _ _ _  

If N-notation is followed, the matrix K s

 

 would be

obtained as

1 1

0 ₂ 1 ₂ 2

K K N N

s

 

 __ _  _  _    

  _  _

The first term in the curly brackets of the above equation i.e. K0is independent of the displacements  . N1is

linearly dependent upon

 

 and

2

_ 

  is quadratically

dependent upon

 

 . The matrix K s

 

 is known as secant

stiffness matrix. The secant stiffness matrix obtained with B-notation is un-symmetric and that obtained with N-notation is symmetric. The correlation between the two notations is expressed as

 

0

T

K B D B dv

L L v  _{   }       

 

1 T T _T

N B D B B D B G S G dv

L NL NL L L

v  _ _{ } _   __{ }_  _  _   __   _          _

 

2 T _T

N B D B G S G dv

NL NL NL

v

_ _ _ _ _ _ 

 _{ }_{ }_ _ __

  _      _

The matrices  S and SNLtogether give symmetric stress

matrix. The symmetric stress matrix is introduced as  S _S_L_{ }S_NL_

And non-linear stiffness matrix

1 1

1 2

2 3

K N N

NL  _  _         =

 

1 1 2 2

T T T

B D B B D B B D B

NL L L NL NL NL

v

_ _ _ _ _ _ _ _ _ _ _ _

 

 

 _           _

D. Mass Matrix

From the above relation, the mass matrix is obtained as

 

_M

 

_NT _G T _G

 

_{N dxdydz}

P P P

V



        _ _{ } _{ } _

   

_M _NT _m

 

_{N dxdy} P

    _ _

The mass matrix thus obtained above is known as consistent mass matrix.

V. ELEMENT STIFFNESS MATRIX

A. Linear element stiffness matrix

The element stiffness matrix for the plate is generated by the subroutine ELSM. The element stiffness matrix for the plate is generated and assembled in as a single array using skyline procedure. The material properties are read from main program. Subroutine ELSM generates BL needed

for evaluation of the element stiffness matrix. The linear

stiffness matrix of the element

 

KL is given by

      

1

T

L L L

K B D B J d d

 



(4)

471

B. Non-linear element stiffness matrix

The non-linear element stiffness matrix



KNL



for the plane

is generated by subroutine ELSMN. The expression for the non-linear element stiffness matrix is





   

1 2

1 1

2 3

NL

K  N  N

Various matrices involved in the above equation are generated by the subroutine ELSMN. The integration of the products is performed by GAUSS subroutine which is based on Gauss quadrature. The non-linear stiffness matrix is renewed iteratively as the element stiffness is formed using the latest value displacement. Then the stiffness matrix is assembled and overall stiffness matrix formed.

VI. BENCH MARK,NATURAL FREQUENCY AND MODE SHAPE RESULT

Comprehensive bench mark analytic solutions of natural frequency and mode shape results are presented.Table 1-3, 4-6, 7-9 and 10-12 list of first 10 frequency parameter of solutions for the “CCCC”, “SSSS”. “CSCS” and “CCCF” plates with varying h/a ratio respectively. The Poisson’s

ratio (µ) is 0.3 and Young’s modulus (E) is 10920pa. The five different size ratio b/a are taken1-5.

Figure 1: A comparison of first ten frequency parameters of CCCC plate

with different mesh a G 

[image:4.612.328.558.106.283.2]

  from FEM with analytical solution

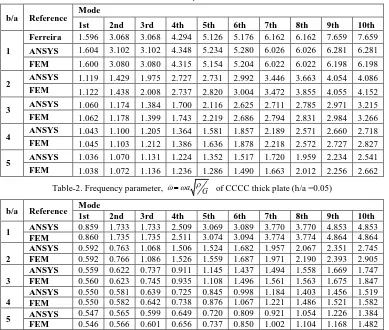
Table-1.Frequency parameter,  a _G of CCCC thick plate (h/a =0.1)

b/a Reference Mode

1st 2nd 3rd 4th 5th 6th 7th 8th 9th 10th

1

Ferreira 1.596 3.068 3.068 4.294 5.126 5.176 6.162 6.162 7.659 7.659

ANSYS 1.604 3.102 3.102 4.348 5.234 5.280 6.026 6.026 6.281 6.281

FEM 1.600 3.080 3.080 4.315 5.154 5.204 6.022 6.022 6.198 6.198

2 ANSYS 1.119 1.429 1.975 2.727 2.731 2.992 3.446 3.663 4.054 4.086

FEM 1.122 1.438 2.008 2.737 2.820 3.004 3.472 3.855 4.055 4.152

3 ANSYS 1.060 1.174 1.384 1.700 2.116 2.625 2.711 2.785 2.971 3.215

FEM 1.062 1.178 1.399 1.743 2.219 2.686 2.794 2.831 2.984 3.266

4 ANSYS 1.043 1.100 1.205 1.364 1.581 1.857 2.189 2.571 2.660 2.718

FEM 1.045 1.103 1.212 1.386 1.636 1.878 2.218 2.572 2.727 2.827

5 ANSYS 1.036 1.070 1.131 1.224 1.352 1.517 1.720 1.959 2.234 2.541

FEM 1.038 1.072 1.136 1.236 1.286 1.490 1.663 2.012 2.256 2.662

Table-2. Frequency parameter,   a _G of CCCC thick plate (h/a =0.05)

1 ANSYS 0.859 1.733 1.733 2.509 3.069 3.089 3.770 3.770 4.853 4.853

FEM 0.860 1.735 1.735 2.511 3.074 3.094 3.774 3.774 4.864 4.864

2

ANSYS 0.592 0.763 1.068 1.506 1.524 1.682 1.957 2.067 2.351 2.745

FEM 0.592 0.766 1.086 1.526 1.559 1.687 1.971 2.190 2.393 2.905

3

ANSYS 0.559 0.622 0.737 0.911 1.145 1.437 1.494 1.558 1.669 1.747

FEM 0.560 0.623 0.745 0.935 1.108 1.496 1.561 1.563 1.675 1.847

4

ANSYS 0.550 0.581 0.639 0.725 0.845 0.998 1.184 1.403 1.456 1.519

FEM 0.550 0.582 0.642 0.738 0.876 1.067 1.221 1.486 1.521 1.582

5 ANSYS 0.547 0.565 0.599 0.649 0.720 0.809 0.921 1.054 1.226 1.384

[image:4.612.114.503.353.683.2]

(5)

472

Table-3. Frequency parameter,   a _G of CCCC thick plate (h/a =0.01)

1

Ferreira 0.175 0.364 0.364 0.536 0.667 0.667 0.827 0.827 1.088 1.088

ANSYS 0.178 0.363 0.363 0.536 0.664 0.665 0.827 0.827 1.088 1.088

FEM 0.177 0.364 0.364 0.536 0.664 0.667 0.827 0.827 1.088 1.088

2 ANSYS 0.121 0.156 0.220 0.313 0.318 0.352 0.412 0.434 0.499 0.584

FEM 0.121 0.157 0.224 0.318 0.324 0.353 0.415 0.461 0.508 0.624

3 ANSYS 0.114 0.127 0.151 0.187 0.236 0.297 0.311 0.325 0.349 0.372

FEM 0.114 0.127 0.152 0.192 0.249 0.312 0.325 0.326 0.351 0.388

4 ANSYS 0.112 0.119 0.130 0.148 0.173 0.205 0.244 0.290 0.309 0.317

FEM 0.112 0.119 0.131 0.151 0.180 0.220 0.273 0.309 0.317 0.330

5 ANSYS 0.133 0.140 0.149 0.164 0.184 0.191 0.218 0.277 0.353 0.355

FEM 0.111 0.115 0.123 0.134 0.151 0.174 0.206 0.248 0.303 0.309

Table-4. Frequency parameter,   a _Gof SSSS thick plate (h/a =0.1)

1

Ferreira 0.935 2.256 2.256 3.460 4.305 4.305 5.356 5.356 6.945 6.945

ANSYS 0.904 2.213 2.213 3.367 4.265 4.271 5.256 5.256 6.025 6.025

FEM 0.935 2.244 2.247 3.450 4.250 4.253 5.311 5.318 6.022 6.022

2 ANSYS 0.580 0.908 1.456 1.918 2.204 2.205 2.687 3.129 3.456 3.956

FEM 0.591 0.938 1.511 1.932 2.247 2.304 2.769 3.311 3.495 3.977

3 ANSYS 0.522 0.666 0.910 1.253 1.688 1.866 1.994 2.208 2.403 2.509

FEM 0.527 0.586 0.944 1.218 1.704 1.873 2.015 2.251 2.408 2.587

4 ANSYS 0.501 0.582 0.718 0.911 1.160 1.461 1.812 1.848 2.016 2.040

FEM 0.504 0.592 0.741 0.953 1.137 1.495 1.853 1.932 2.034 2.066

5 ANSYS 0.492 0.543 0.630 0.753 0.912 1.107 1.335 1.694 1.839 1.885

FEM 0.494 0.550 0.645 0.782 0.965 1.117 1.330 1.649 1.847 1.894

Table-5. Frequency parameter,   a _G of SSSS thick plate (h/a =0.05)

1 ANSYS 0.471 1.178 1.178 1.853 2.350 2.351 2.987 2.987 3.971 3.971

FEM 0.480 1.190 1.192 1.885 2.365 2.367 3.026 3.033 3.989 3.991

2

ANSYS 0.298 0.473 0.768 1.014 1.181 1.181 1.463 1.710 1.860 2.195

FEM 0.300 0.481 0.787 1.017 1.193 1.225 1.489 1.806 1.914 2.199

3

ANSYS 0.266 0.343 0.474 0.657 0.894 0.983 1.057 1.182 1.182 1.358

FEM 0.267 0.348 0.484 0.682 0.946 0.984 1.063 1.195 1.286 1.386

4

ANSYS 0.255 0.298 0.371 0.474 0.607 0.769 0.961 0.972 1.014 1.084

FEM 0.256 0.301 0.378 0.489 0.639 0.793 0.973 1.017 1.076 1.092

5 ANSYS 0.250 0.278 0.324 0.389 0.474 0.578 0.701 0.843 0.967 0.994

FEM 0.250 0.279 0.329 0.400 0.496 0.620 0.777 0.968 0.974 0.996

Table-6. Frequency parameter,   a _G of SSSS thick plate (h/a =0.01

1

Ferreira 0.097 0.243 0.243 0.389 0.493 0.493 0.638 0.638 0.855 0.855

ANSYS 0.097 0.245 0.245 0.392 0.503 0.503 0.649 0.648 0.888 0.888

FEM 0.097 0.243 0.244 0.390 0.493 0.494 0.638 0.641 0.856 0.856

2 ANSYS 0.060 0.097 0.157 0.207 0.243 0.243 0.303 0.355 0.389 0.457

FEM 0.060 0.097 0.160 0.207 0.244 0.251 0.306 0.373 0.396 0.457

3 ANSYS 0.054 0.070 0.097 0.134 0.183 0.200 0.216 0.243 0.243 0.281

FEM 0.054 0.070 0.098 0.138 0.193 0.200 0.217 0.244 0.263 0.284

4 ANSYS 0.051 0.060 0.075 0.097 0.124 0.157 0.197 0.198 0.207 0.222

FEM 0.051 0.061 0.076 0.099 0.129 0.169 0.198 0.207 0.220 0.223

5 ANSYS 0.050 0.056 0.066 0.079 0.097 0.118 0.143 0.172 0.100 0.203

(6)

473

Table-7.Frequency parameter,   a _G of CSCS thick plate (h/a =0.1)

1

Ferreira 1.295 2.398 2.930 3.841 4.350 5.138 5.512 5.899 6.951 7.298

ANSYS 1.301 2.413 2.946 3.882 4.373 5.167 5.582 5.975 6.025 6.026

FEM 1.311 2.423 2.941 3.904 4.338 5.104 5.579 5.951 6.022 6.022

2 ANSYS 0.642 1.078 1.729 1.944 2.295 2.554 2.858 3.497 3.605 3.970

FEM 0.651 1.107 1.786 1.955 2.329 2.671 2.927 3.538 3.753 3.988

3 ANSYS 0.540 0.727 1.021 1.701 1.874 1.885 2.022 2.267 2.439 2.604

FEM 0.544 0.742 1.056 1.482 1.880 2.023 2.040 2.306 2.485 2.686

4 ANSYS 0.509 0.609 0.771 0.992 1.267 1.593 1.851 1.932 1.965 2.066

FEM 0.511 0.619 0.795 1.039 1.357 1.657 1.856 1.943 1.993 2.142

5 ANSYS 0.495 0.557 0.659 0.799 0.976 1.188 1.432 1.709 1.841 1.891

FEM 0.497 0.564 0.675 0.832 1.038 1.299 1.622 1.748 1.900 1.992

Table-8. Frequency parameter,   a _G

of CSCS thick plate (h/a =0.05)

1 ANSYS 0.692 1.302 1.640 2.205 2.426 3.019 3.239 3.556 4.022 4.514

FEM 0.695 1.309 1.646 2.219 2.435 3.029 3.259 3.576 4.033 4.542

2

ANSYS 0.331 0.567 0.926 1.028 1.235 1.398 1.569 1.983 2.023 2.203

FEM 0.333 0.576 0.950 1.031 1.245 1.460 1.596 2.085 2.116 2.207

3

ANSYS 0.276 0.375 0.533 0.745 0.987 1.009 1.074 1.217 1.324 1.414

FEM 0.277 0.380 0.547 0.778 0.989 1.079 1.081 1.230 1.350 1.465

4

ANSYS 0.259 0.313 0.399 0.517 0.666 0.844 0.970 1.021 1.051 1.099

FEM 0.259 0.315 0.407 0.538 0.655 0.929 0.975 1.024 1.107 1.204

5 ANSYS 0.252 0.285 0.339 0.414 0.508 0.622 0.755 0.907 0.968 0.997

FEM 0.252 0.287 0.345 0.427 0.537 0.677 0.855 0.969 1.000 1.052

Table-9. Frequency parameter,   a _G

of CSCS thick plate (h/a =0.01)

1

Ferreira 0.142 0.271 0.349 0.472 0.519 0.671 0.708 0.795 0.899 1.023

ANSYS 0.140 0.271 0.349 0.473 0.520 0.672 0.710 0.796 0.900 1.026

FEM 0.142 0.270 0.344 0.468 0.510 0.652 0.698 0.777 0.868 1.001

2 ANSYS 0.067 0.116 0.190 0.210 0.254 0.290 0.326 0.415 0.426 0.459

FEM 0.067 0.117 0.194 0.210 0.255 0.302 0.330 0.436 0.444 0.459

3 ANSYS 0.055 0.076 0.109 0.152 0.201 0.207 0.220 0.250 0.273 0.293

FEM 0.056 0.077 0.111 0.158 0.201 0.220 0.221 0.252 0.298 0.303

4 ANSYS 0.052 0.063 0.081 0.105 0.136 0.173 0.198 0.212 0.216 0.225

FEM 0.052 0.063 0.082 0.109 0.144 0.190 0.198 0.209 0.226 0.247

5 ANSYS 0.051 0.057 0.069 0.084 0.103 0.127 0.154 0.186 0.197 0.203

FEM 0.051 0.058 0.069 0.086 0.109 0.137 0.174 0.197 0.204 0.214

Table-10. Frequency parameter,   a _G of CFFF thick plate (h/a =0.1)

1

Ferreira 1.093 1.757 2.735 3.261 3.356 3.860 4.642 4.977 5.373 5.465

ANSYS 1.092 1.758 2.692 3.259 3.354 3.853 4.648 4.955 5.364 5.453

FEM 1.088 1.751 2.700 3.232 3.326 3.850 4.605 4.866 5.360 5.367

2 ANSYS 1.035 1.176 1.505 2.052 2.645 2.796 2.809 3.104 3.264 3.582

FEM 1.036 1.179 1.512 2.081 2.654 2.804 2.890 3.114 3.271 3.603

3 ANSYS 1.062 1.086 1.215 1.433 1.654 2.167 2.639 2.676 2.838 2.900

FEM 1.029 1.088 1.219 1.446 1.790 2.262 2.648 2.714 2.845 2.869

4 ANSYS 1.028 1.057 1.125 1.236 1.400 1.619 1.896 2.418 2.610 2.637

FEM 1.027 1.059 1.127 1.243 1.420 1.670 2.005 2.434 2.646 2.683

5 ANSYS 1.024 1.045 1.086 1.153 1.250 1.380 1.547 1.751 1.990 2.662

(7)

474

1 ANSYS 0.575 0.949 1.505 1.809 1.889 2.692 2.294 3.146 3.251 3.848

FEM 0.575 0.948 1.506 1.808 1.888 2.688 2.879 3.147 3.252 3.850

2

ANSYS 0.546 0.630 0.807 1.112 1.476 1.545 1.566 1.751 2.105 2.152

FEM 0.546 0.625 0.809 1.127 1.477 1.568 1.593 1.755 2.053 2.215

3

ANSYS 0.542 0.574 0.645 0.765 0.941 1.173 1.465 1.472 1.512 1.591

FEM 0.542 0.574 0.647 0.772 0.963 1.229 1.474 1.513 1.580 1.593

4

ANSYS 0.541 0.558 0.595 0.657 0.741 0.867 1.022 1.205 1.423 1.471

FEM 0.541 0.558 0.596 0.661 0.758 0.896 1.084 1.329 1.473 1.495

5 ANSYS 0.540 0.551 0.574 0.611 0.664 0.735 0.827 0.968 1.169 1.458

FEM 0.540 0.551 0.575 0.613 0.671 0.753 0.865 1.014 1.207 1.455

1

Ferreira 0.118 0.197 0.319 0.383 0.403 0.584 0.639 0.725 0.882 0.905

ANSYS 0.118 0.197 0.320 0.383 0.404 0.585 0.639 0.692 0.725 0.883

FEM 0.117 0.196 0.314 0.379 0.398 0.577 0.619 0.675 0.705 0.863

2 ANSYS 0.111 0.128 0.165 0.229 0.308 0.321 0.327 0.368 0.431 0.441

FEM 0.111 0.128 0.166 0.233 0.308 0.327 0.331 0.368 0.434 0.466

3 ANSYS 0.110 0.117 0.132 0.157 0.193 0.242 0.303 0.307 0.315 0.332

FEM 0.110 0.117 0.132 0.158 0.198 0.254 0.307 0.316 0.328 0.333

4 ANSYS 0.110 0.114 0.121 0.134 0.153 0.178 0.210 0.249 0.294 0.307

FEM 0.110 0.114 0.122 0.135 0.155 0.184 0.224 0.275 0.307 0.312

5 ANSYS 0.110 0.112 0.118 0.117 0.140 0.154 0.177 0.209 0.235 0.376

FEM 0.110 0.112 0.117 0.125 0.137 0.154 0.178 0.209 0.250 0.303

VII. COMPARISON OF NUMERICAL AND EXPERIMENTAL RESULT

Here, we have considered five different lengths to breadth ratios b/a ranging from 1 to 5 and each ratio ten numerical frequency results are given for each type of plate. After calculated, the present solutions of Eigen frequencies are able to easily validate with the FEM results by using ANSYS software, where we have chosen rectangular thick plate, and considered the mesh size in equivalently (15x15). We note that we could actually use this boundary condition for clamped and simply supported

boundary conditions, the present results match pretty well of the other researchers. After we may sum up of all results, concluded that the Eigen frequencies are decreasing with increase in the thickness to length ratio (h/a) and are increasing with the increase in the b/a ratio in the face of the boundary condition assumed. Here presented the some deflected mode shape with reference to the Eigen frequencies for free vibration of thick isotropic rectangular plates with different boundary condition such as “CCCC”, “SSSS”, “CSCS”, “CCCF” are established respectively in fig(2-5).

(8)

475

FEM

ANSYS

[image:8.612.61.535.51.333.2]

FEM

Figure 2: Comparison of FEM (top) and ANSYS (bottom) solution of first ten mode shapes of isotopic plate (b/a = 1 and h/a = 0.01) with boundary condition CCCC. The ten mode shapes are presented in two rows.

ANSYS

FEM

(9)

[image:9.612.77.534.51.135.2]

476

FEM

Figure 3: Comparison of FEM (top) and ANSYS (bottom) solution of first ten mode shapes of isotopic plate (b/a = 1 and h/a = 0.01) with boundary condition SSSS. The ten mode shapes are presented in two rows.

ANSYS

FEM

ANSYS

FEM

Figure 4: Comparison of FEM (top) and ANSYS (bottom) solution of first ten mode shapes of isotopic plate (b/a = 1 and h/a = 0.01) with boundary condition CSCS. The ten mode shapes are presented in two rows.

[image:9.612.48.535.166.557.2]

(10)

477

FEM

ANSYS

[image:10.612.48.535.51.307.2]

FEM

Figure 5: Comparison of FEM (top) and ANSYS (bottom) solution of first ten mode shapes of isotopic plate (b/a = 1 and h/a = 0.01) with boundary condition CFFF. The ten mode shapes are presented in two rows.

VIII. CONCLUSION

In this paper, Non-linear free vibration of isotropic thick rectangular plate is investigated with four proposed different boundary condition. The study is carried out following a novel method in which static analysis serves as the basis for the subsequent dynamic study. Calculations for different boundary condition of modal analysis are performed and results compared with the available literature to validate the present model. Comprehensive “FEM” and the software we are using “ANSYS” validated analytic natural frequency and mode shapes results are listed and very fast convergence regardless of the order of the mode. The solution convergence with the number of degree freedom, which is generalized co-ordinate in the expansion of the plate displacement. We also conclude that length-breadth ratio (b/a) and thickness to length ratio (h/a) are crucial factor that decide the nature of frequency and modes of free vibration of isotropic thick rectangular plate.

Reference

[1] Abdalla, J.A. and lbrahim, A.K. (2007). A geometrically nonlinear thick plate bending element based on mixed formulation and discrete collocation constraints. Structural Engineering and Mechanics, Vol. 26, No. 6, PP 1-15.

[2] Panda, S. and Barik, M. (2016). Finite element dynamic analysis of thin plates with complicated geometr. Proceedings of 24th ISERD International Conference, PP 41-44.

[3] Wang, C.M. Lim, G.T. Reddy, J.N. and Lee. K.H. (2001). Relationships between bending solutions of Reissner and Mindlin plate theories. Engineering Structures 23, PP 838–849.

[4] Lim, C.W. Lü, C.F. Xiang, Y. and Yao, W. (2009). On new symplectic elasticity approach for exact free vibration solutions

of rectangular Kirchhoff plates. International Journal of Engineering Science 47, PP 131–140.

[5] Hansbo, P. Heintz, D. and Larson, M.G. (2011). A finite element method with discontinuous rotations for the Mindlin– Reissner plate model. Comput. Methods Appl. Mech. Engrg. Vol 200, PP 638–648.

[6] Xing, Y. and Liu, B. (2009). Characteristic equations and closed-form solutions for free vibrations of rectangular mindlin plates. Acta Mechanica Solida Sinica, Vol. 22, No. 2, PP 125-136.

[7] Thai, H.T. and Choi, D.H. (2013). Analytical solutions of refinedplate theory for bending,buckling and vibration analyses of thick plates. Applied Mathematical Modelling. PP 1-13.

[8] Pradhan, K.K. and Chakraverty, S. (2015). Transverse vibration of isotropic thick rectangular plates based on new inverse trigonometric shear deformation theories. International Journal of Mechanical Sciences, vol 94-95, PP 211–231.

[9] Lezgy-Nazargah, M. (2016). A high-performance parametrized mixed finite element model for bending and vibration analyses of thick plates. Acta Mech DOI 10.1007/s00707-016-1676-4. © Springer-Verlag Wien 2016.

[10] Senjanovic´, I. Tomic´, M. Hadzˇic´, N. and Vladimir, N. (2017). Dynamic finite element formulations for moderately thick plate vibrations based on the modified Mindlin theory. Engineering Structures 136 . PP 100–113.

(11)

478

[12] Li, R. Wang, P. Xue, R. and Guo, X. (2017). New analytic

solutions for free vibration of rectangular thick plates with an edge free. International Journal of Mechanical Sciences 131– 132. PP 179–190.

[13] Saha, K.N. Misra, D. Ghosal, S. and Pohit, G. (2005). Nonlinear free vibration analysis of square plates with various boundary conditions. Journal of Sound and Vibration 287. PP 1031–1044.

[14] Amabili, M. (2004). Nonlinear vibrations of rectangular plates with different boundary conditions: theory and experiments. Computers and Structures 82. PP 2587–2605.

[15] Wu, J.J. (2003). Vibration of a rectangular plate undergoing forces moving along a circular path. Finite Elements in Analysis and Design 40. PP 41–60.

[16] Talha, M. and Singh, B.N. (2010). Static response and free vibration analysis of FGM plates using higher order shear deformation theory. Applied Mathematical Modelling 34. PP 3991–4011.

[17] Leung, A.Y.T. and Zhu, B. (2004). Geometric nonlinear vibration of clamped Mindlin plates by analytically integrated trapezoidal p-element. Thin-Walled Structures 42. PP 931–945.

[18] Xiang, Y. and Kitipornchai, S. (1995). Research on thick plate vibration: a literature survey. Journal of Sound and Vibration. Vol 180(1). PP 163-176.

[19] Oaate, E. Zienkiewicz, O.C. Suarez, B. and Taylor, R.L. (1992). A general methodology for deriving shear constrained reissner-mindlin plate elements. International journal for numerical methods in engineering, VOL. 33, PP 345-367.

[20] Zienkiewicz, O.C. Taylor, R.L. Papadopouls, P. and Onate, E. (1990). Plate bending elements with discrete constraints: new triangular elements. Compurrrs & Srructures Vol. 35. No. 4, pp. 505-522.

[21] Cen, S and Shang, Y (2015) Developments of Mindlin-Reissner Plate Elements. Hindawi Publishing Corporation,Mathematical Problems in Engineering,

[22] Ribeiro P and Akhavan H (2012) Non-linear vibrations of variable stiffness composite laminated plates, Composite Structures,PP-2424–2432.

[23] Guoyong J, Zhu S, Shuangxia S, Tiangui Y, Siyang G (2013) ” Three-dimensional exact solution for the free vibration of arbitrarily thick functionally graded rectangular plates with general boundary conditions”, Composite Structures, Accepted Manuscript.

[24] Abdalla J.A, Ibrahim A.M(2006) “Development of a discrete

Reissner–Mindlin element on Winkler foundation”, Finite Elements in Analysis and Design ,PP-740 – 748,

[25] Malekzadeh P, Karami G. (2004) “Vibration of non-uniform thick plates on elastic foundation by differential quadrature method”, Engineering Structures PP-1473–1482

[26] liew k. m., xiang ,y. and kitipornchai$ s.(1993) “transverse vibration of thick rectangular plates-i. comprehensive sets of

boundary conditions”, Computers& Structures Vol. 49, No. I, pp. l-29.

[27] Mishra a.k (2008) “ finite element large amplitude free flexural vibration analysis of isotropic plates”, Department of civil engineering National institute of technology Rourkela-769008, thesis.