Edge Vertex Dominating Sets and Edge Vertex Domination Polynomials of Cycles

(1)

http://dx.doi.org/10.4236/ojdm.2015.54007

Edge-Vertex Dominating Sets and

Edge-Vertex Domination Polynomials

of Cycles

A. Vijayan1, J. Sherin Beula2

1_{Department of Mathematics, Nesamony Memorial Christian College, Marthandam, India}

2_{Department of Mathematics, Mar Ephraem College of Engineering & Technology, Marthandam, India} Email: dravijayan@gmail.com, sherinbeula@gmail.com

Received 27 March 2015; accepted 27 September 2015; published 30 September 2015

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

Abstract

Let G = (V, E) be a simple graph. A set S⊆E(G) is an edge-vertex dominating set of G (or simply an ev-dominating set), if for all vertices v ∈V(G); there exists an edge e∈S such that e dominates v. Let

(

)

ev n

D C i, denote the family of all ev-dominating sets of Cn with cardinality i. Let

(

)

(

)

ev n ev n

d C i, = D C i, . In this paper, we obtain a recursive formula for d C i_ev

(

_n,

)

. Using this

re-cursive formula, we construct the polynomial,

(

)

_{ }

(

)

   

∑

n i

ev n _i n ev n

D C x d C i x

4

, ,

=

= , which we call edge-

vertex domination polynomial of Cn (or simply an ev-domination polynomial of Cn) and obtain

some properties of this polynomial.

Keywords

ev-Domination Set, ev-Domination Number, ev-Domination Polynomials

1. Introduction

Let G = (V, E) be a simple graph of order |V| = n. A set S⊆V(G) is a dominating set of G, if every vertex V S\ is adjacent to at least one vertex in S. For any vertex v ∈ V, the open neighbourhood of ν is the set

( ) {

}

N v = u V uv E∈ ∈ and the closed neighbourhood of ν is the set N v

[ ]

=N v

( ) { }

∪ v . For a set S⊆V, the open neighbourhood of S is N S

( )

=U N vv S∈

( )

and the closed neighbourhood of S is N S

[ ]

=N S

( )

∪S. The domination number of a graph G is defined as the minimum size of a dominating set in G and it is denoted as

( )

G

(2)

Definition 1.1

For a graph G = (V, E), an edge e uv E G= ∈

( )

, ev-dominates a vertex w V G∈

( )

if 1) u = w or v = w (w is incident to e) or

2) uw or vw is an edge in G (w is adjacent to u or v). Definition 1.2 [1]

A set S E G⊆

( )

is an edge-vertex dominating set of G (or simply an ev-dominating set), if for all vertices

( )

v V G∈ ; there exists an edge e S∈ such that e dominates v. The ev-domination number of a graph G is de-fined as the minimum size of an ev-dominating set of edges in G and it is denoted as γev

( )

G .

Definition 1.3

Let D C iev

(

n,

)

be the family of ev-dominating sets of a graph Cn with cardinality i and let

(

,

)

(

,

)

ev n ev n

d C i = D C i . We call the polynomial

(

)

(

)

4

, n , i

ev n _i n ev n

D C x  d C i x

= _{ }

=

∑

the ev-domination poly-nomial of the graph Cn.

In the next section, we construct the families of the ev-dominating sets of cycles by recursive method. As usual we use   x for the largest integer less than or equal to x and   x for the smallest integer greater than or equal to x. Also, we denote the set

{

e e1, , ,2 en

}

by [en] and the set

{

1,2, , n

}

by [n], throughout this pa-per.

2. Edge-Vertex Dominating Sets of Cycles

Let D C iev

(

n,

)

be the family of ev-dominating sets of Cn with cardinality i. We investigate the ev-dominating sets of Cn. We need the following lemma to prove our main results in this section.

Lemma 2.1: [2]

( )

4

ev Cn n

γ _{=  } 

 .

By Lemma 2.1 and the definition of ev-domination number, one has the following Lemma: Lemma 2.2: D C iev

(

n,

)

= Φ if and only if i n> or i ₄n

  <  _{ }.

Lemma 2.3: If a graph G contains a simple path of length 4k− 1, then every ev-dominating set of G must contain at least k vertices of the path.

Proof: The path has 4k vertices. As every edge dominates at most 4 vertices, the 4k vertices are covered by at least k edges.

Lemma 2.4. If Y D C∈ ev

(

n−5, 1i−

)

, and there exists x∈ [en] such that Y∪

{ }

x ∈D C iev

(

n,

)

then

(

4, 1

)

ev n

Y D C∈ − i− .

Proof: Suppose that Y D C∉ ev

(

n−4, 1i−

)

. Since Y D C∈ ev

(

n−5, 1i−

)

, Y contains at least one edge labelled en−5, en−6 or en−7.

If en−5∈Y, then Y D C∈ ev

(

n−4, 1i−

)

, a contradiction. Hence en−6 or en−7∈Y, but then in this case

{ }

ev

(

n,

)

Y∪ x ∉D C i for any x∈ [en], also a contradiction. Lemma 2.5. [3]

1) If D Cev

(

n−1, 1i− =

)

D Cev

(

n−4, 1i− = Φ

)

then D Cev

(

n−2, 1i− =

)

D Cev

(

n−3, 1i− = Φ

)

.

2) If D Cev

(

n−1, 1i− ≠ Φ

)

, and D Cev

(

n−4, 1i− ≠ Φ

)

then D Cev

(

n−2, 1i− ≠ Φ

)

and D Cev

(

n−3, 1i− ≠ Φ

)

. 3) If D Cev

(

n−₁, 1i− = Φ

)

, D Cev

(

n−2, 1i− = Φ

)

, D Cev

(

n−3, 1i− = Φ

)

, and D Cev

(

n−4, 1i− = Φ

)

, then

(

,

)

ev n

D C i = Φ.

Proof: 1) Since D Cev

(

n−1, 1i− =

)

D Cev

(

n−4, 1i− = Φ

)

, by Lemma 2.2, i− > −1 n 1 or

4 1

4 n i_{− < } − _

 . In

ei-ther case, we have D Cev

(

n−₂, 1i− = Φ

)

and D Cev

(

n−3, 1i− = Φ

)

.

2) Since D Cev

(

n−1, 1i− ≠ Φ

)

and D Cev

(

n−4, 1i− ≠ Φ

)

, by Lemma 2.2, we have

1 ₁ ₁

4

n− _i _n

 _{ ≤ − ≤ −}

 

  and

4 ₁ ₄

4

n− _i _n

 _{ ≤ − ≤ −}

 

  . Hence

2 ₁ ₂

4

n− _i _n

 _{ ≤ − ≤ −}

 

  and

3 ₁ ₃

4

n− _i _n

 _{ ≤ − ≤ −}

 

(3)

(

2, 1

)

ev n

D C− i− ≠ Φ and D Cev

(

n−3, 1i− ≠ Φ

)

.

3) By hypothesis, i− > −1 n 1 or 1 4 4 n i_{− < } − _

 . Therefore, i n> or 44 1 n i<_ − _+

  . Therefore, i n> or

4 n i_{<  } 

 . Therefore, D C iev

(

n,

)

= Φ.

Lemma 2.6. [4] If D C iev

(

n,

)

≠ Φ, then

1) D Cev

(

n−1, 1i− =

)

D Cev

(

n−2, 1i− =

)

D Cev

(

n−3, 1i− = Φ

)

and D Cev

(

n−4, 1i− ≠ Φ

)

if and only if n = 4k and i = k for some k∈N.

2) D Cev

(

n−2, 1i− =

)

D Cev

(

n−3, 1i− =

)

D Cev

(

n−4, 1i− = Φ

)

and D Cev

(

n−1, 1i− ≠ Φ

)

if and only if i = n. 3) D Cev

(

n−1, 1i− = Φ

)

, D Cev

(

n−2, 1i− ≠ Φ

)

, D Cev

(

n−3, 1i− ≠ Φ

)

, D Cev

(

n−4, 1i− ≠ Φ

)

, if and only if n =

4k + 2 and 4 2 4 k i_{= } + _

  for some k ∈N.

4) D Cev

(

n−1, 1i− ≠ Φ

)

, D Cev

(

n−2, 1i− ≠ Φ

)

, D Cev

(

n−3, 1i− ≠ Φ

)

and D Cev

(

n−4, 1i− = Φ

)

if and only if i = n – 2.

5) D Cev

(

n−1, 1i− ≠ Φ

)

, D Cev

(

n−2, 1i− ≠ Φ

)

, D Cev

(

n−3, 1i− = Φ

)

and D Cev

(

n−4, 1i− ≠ Φ

)

if and only if i = n – 1.

6) D Cev

(

n−1, 1i− ≠ Φ

)

, D Cev

(

n−2, 1i− ≠ Φ

)

, D Cev

(

n−3, 1i− ≠ Φ

)

and D Cev

(

n−4, 1i− ≠ Φ

)

if and only if

1 1 3

4

n− _{i n}

 _{ + ≤ ≤ −}

 

  .

Proof: 1) (⇒) Since D Cev

(

n−1, 1i− =

)

D Cev

(

n−2, 1i− =

)

D Cev

(

n−3, 1i− = Φ

)

, by Lemma 2.2, i− > −1 n 1 or 3

1 4 n i_{− < } − _

 . If i− > −1 n 1, then i n> and by Lemma 2.2, D C iev

(

n,

)

= Φ, a contradiction.

So

3 1

4 n i_{− < } − _

  (2.1)

and since D Cev

(

n−4, 1i− ≠ Φ

)

, we have

4 ₁ ₄

4

n− _i _n

 _{ ≤ − ≤ −}

 

  (2.2)

From (2.1) and (2.2),

4 ₁ 3

4 4

n− _i n−

 _{≤ − <} 

   

    (2.3)

When n is a multiple of 4, 4 1

4 4

n− n

 _{ = −}

 

  and

3

4 4

n− n

 _{ =}

 

  . Therefore, 4 1 1 4

n_{− ≤ − <}_i n _{. Therefore,}

1 1

4 n

i− = − , we get 4 n

i= . Thus, when n=4k, (2.3) holds good and 4 n

i= =k. When n≠4k,

4 ₁

4 4

n− n

   ₌ ₋

   

    and

3 ₁

4 4

n− n

   ₌ ₋

   

    . Therefore, 4 1 1 4 1

n _i n

 _{− ≤ − <} ₋

   

    , which is not possible.

Hence n=4k and i k=

(⇐) If n = 4k and i = k for some k ∈ N, then by Lemma 2.2, 1 4 1 1

4 4

n− k− _{k i i}

  ₌ _{= = > −}

   

    . Therefore,

1 1

4 n i_{− < } − _

(4)

Now 4 4 4 1 1

4 4

n− k− _k _i

  ₌ _{= − = −}

   

4 ₁

4

n− _i

 _{ ≤ −}

 

  , which implies D Cev

(

n−4, 1i− ≠ Φ

)

.

2) (⇒) Since D Cev

(

n−2, 1i− =

)

D Cev

(

n−3, 1i− =

)

D Cev

(

n−4, 1i− = Φ

)

, by Lemma 2.2, i− > −1 n 2 or 4

1 4 n i_{− < } − _

 . If

4 1

4 n i_{− < } − _

  then by Lemma 2.2, D Cev

(

n−1, 1i− = Φ

)

, a contradiction.

So

1 2

i− > −n (2.4) Since,

(

1, 1

)

ev n

D C − i− ≠ Φ,

1 ₁ ₁

4

n− _i _n

 _{ ≤ − ≤ −}

 

  (2.5)

From (2.4) and (2.5), we have n− ≥ − > −1 i 1 n 2. Therefore, i− = −1 n 1. Therefore, i n=

(⇐) If i n= , then by Lemma 2.2, 4

n _{i n}

  ≤ ≤  

  . Therefore,

1 ₁ ₁

4

n− _i _n

 _{ ≤ − ≤ −}

 

Therefore, D Cev

(

n−1, 1i− ≠ Φ

)

(

n−1, 1i− = Φ

)

, by Lemma 2.2, i− > −1 n 1 or

1 1<

4 n i− _ − _

 . If i− > −1 n 1, then

1 2 3 4

i− > − > − > −n n n , by Lemma 2.2, D Cev

(

n−2, 1i− =

)

D Cev

(

n−3, 1i− =

)

D Cev

(

n−4, 1i− = Φ

)

, a contradic-tion.

Therefore, 1 1 4 n i_{− < } − _

 , which implies,

1 1 4 n i<_ − _+

  (2.6)

Since, D Cev

(

n−2, 1i− ≠ Φ

)

,

2 ₁ ₂

4

n− _i _n

 _{ ≤ − ≤ −}

 

  .

Hence,

2 1 1

4

n− _{i n}

 _{ + ≤ ≤ −}

 

  (2.7)

Similarly,

3 1 2

4

n− _{i n}

 _{ + ≤ ≤ −}

 

  (2.8)

and

4 1 3

4

n− _{i n}

 _{ + ≤ ≤ −}

 

  (2.9)

From (2.6), (2.7), (2.8) and (2.9),

2 ₁ 1 ₁

4 4

n− _i n−

 _{+ ≤ <} ₊

   

    (2.10)

Therefore, (2.10) hold when 2 4 n

k= − or n=4k+2 and 1 4 2 4 k i k_{= + = } + _

 , for some k N∈ . Suppose

4 2

n= k+ , then 2 1 1

4

n− _k

 _{ + = +}

 

  and 41 1 2

n− _k

 _{ + = +}

 

  . Therefore, from (2.10), we have, k+ ≤ < +1 i k 2,

(5)

Case 1) When n=4k.

From (2.10), we get 4 2 1 1 4

k− _k

 _{ + = +}

 

  and 4 1 14 1

k− _k

 _{ + = +}

 

  . Therefore, k+ ≤ < +1 i k 1, which is not

possible.

Case 2) When n=4k+1_{. From (2.10), we get} 4 1 2 1 1 4

k+ − _k

 _{ + = +}

 

  and 4 1 1 14 1

k+ − _k

 _{ + = +}

 

  .

There-fore, k+ ≤ < +1 i k 1, which is not possible.

Case 3) When n=4k+3. From (2.10), we get 4 3 2 1 2 4

k+ − _k

 _{ + = +}

 

  and

4 _{3 1 1} ₂

4

k+ − _k

 _{ + = +}

 

Therefore, k+ ≤ < +2 i k 2, which is not possible. Therefore, n=4k+2 (⇐) If n = 4k + 2 and 4 2

4 k i_{= } + _

  for some k ∈N, and D C iev

(

n,

)

≠ Φ, then by Lemma 2.2, 4

n _{i n}

  ≤ ≤  

  ,

4 2 ₁

4 4

n k+ _{i i}

  ₌ _{= > −}

   

1 1

4 n i_{− < } − _

 . Therefore, D Cev

(

n−1, 1i− = Φ

)

.

Also, 2 4

n− _k

 _{ =}

 

2 ₁ ₂

4

n− _i _n

 _{ ≤ − ≤ −}

 

  and

3 ₁ ₃

4

n− _i _n

 _{ ≤ − ≤ −}

 

  and

4 ₁ ₄

4

n− _i _n

 _{ ≤ − ≤ −}

 

  .

Hence D Cev

(

n−2, 1i− ≠ Φ

)

, D Cev

(

n−3, 1i− ≠ Φ

)

, D Cev

(

n−4, 1i− ≠ Φ

)

. 4) (⇒) Since D Cev

(

n−4, 1i− = Φ

)

, by Lemma 2.2,

1 4

i− > −n or 1 4

4 n i_{− < } − _

  (2.11)

Since D Cev

(

n−3, 1i− ≠ Φ

)

, by Lemma 2.2,

3 ₁ ₃

4

n− _i _n

 _{ ≤ − ≤ −}

 

  (2.12)

Similarly, D Cev

(

n−2, 1i− ≠ Φ

)

and D Cev

(

n−1, 1i− ≠ Φ

)

, by Lemma 2.2

2 ₁ ₂

4

n− _i _n

 _{ ≤ − ≤ −}

 

  (2.13)

and

1 ₁ ₁

4

n− _i _n

 _{ ≤ − ≤ −}

 

  (2.14)

From (2.11), we get 1 4 4 n i_{− < } − _

  which is not possible.

Therefore,

1 4 3 2

i− > − ⇒ > − ⇒ ≥ −n i n i n (2.15) From (2.12),

1 3 2

i− ≤ − ⇒ ≤ −n i n (2.16) From (2.15) and (2.16), i n= −2

(⇐) If i n= −2 , i− = −1 n 3 then by Lemma 2.2, i− > −1 n 4 or 1 4 4 n i_{− < } − _

(

4, 1

)

ev n

D C− i− = Φ. Also

1 ₁ ₁

4

n− _i _n

 _{ ≤ − ≤ −}

 

  ,therefore, D Cev

(

n−1, 1i− ≠ Φ

)

;

2 ₁ ₂

4

n− _i _n

 _{ ≤ − ≤ −}

 

  ,

there-fore, D Cev

(

n−2, 1i− ≠ Φ

)

; and

3 ₁ ₃

4

n− _i _n

 _{ ≤ − ≤ −}

 

  , therefore, D Cev

(

n−3, 1i− ≠ Φ

)

.

(6)

1 4

i− > −n or 1 4

4 n i_{− < } − _

  (2.17)

Since D Cev

(

n−3, 1i− = Φ

)

by Lemma 2.2,

1 3

i− > −n or 1 3

4 n i_{− < } − _

  (2.18)

Since D Cev

(

n−2, 1i− ≠ Φ

)

and D Cev

(

n−1, 1i− ≠ Φ

)

, by Lemma 2.2,

2 ₁ ₂

4

n− _i _n

 _{ ≤ − ≤ −}

 

  (2.19)

and

1 ₁ ₁

4

n− _i _n

 _{ ≤ − ≤ −}

 

  (2.20)

From (2.19) and (2.20), we have 1 1 2 4

n− _i _n

 _{ ≤ − ≤ −}

 

  . From (2.18), we have i− > −1 n 3. Therefore,

1 2

i− ≥ −n . But i− ≤ −1 n 2. Therefore, i− = −1 n 2. Therefore, i n= −1.

(⇐) If i n= −1, i− = −1 n 2 then by Lemma 2.2, D Cev

(

n−3, 1i− = Φ

)

and i− > −1 n 4 therefore,

(

4, 1

)

ev n

D C− i− = Φ and

1 ₁ ₁

4

n− _i _n

 _{ ≤ − ≤ −}

 

  , therefore, D Cev

(

n−1, 1i− ≠ Φ

)

and

2 ₂ ₂

4

n− _i _n

 _{ ≤ − ≤ −}

 

  ,

therefore, D Cev

(

n−2, 1i− ≠ Φ

)

.

(

n−1, 1i− ≠ Φ

)

, D Cev

(

n−2, 1i− ≠ Φ

)

, D Cev

(

n−3, 1i− ≠ Φ

)

, and D Cev

(

n−4, 1i− ≠ Φ

)

, by

Lemma 2.2, 1 1 1

4

n− _i _n

 _{ ≤ − ≤ −}

 

  ,

2 ₁ ₂

4

n− _i _n

 _{ ≤ − ≤ −}

 

  ,

3 ₁ ₃

4

n− _i _n

 _{ ≤ − ≤ −}

 

  , and

4 ₁ ₄

4

n− _i _n

 _{ ≤ − ≤ −}

 

  .

So 1 1 4

4

n− _i _n

 _{ ≤ − ≤ −}

 

  and hence 41 1 3

n− _{i n}

 _{ + ≤ ≤ −}

 

  .

(⇐) If 1 1 3

4

n− _{i n}

 _{ + ≤ ≤ −}

 

  , then by Lemma 2.2 we have,

1 ₁ ₁

4

n− _i _n

 _{ ≤ − ≤ −}

 

  ,

2 ₁ ₂

4

n− _i _n

 _{ ≤ − ≤ −}

 

  ,

3 ₁ ₃

4

n− _i _n

 _{ ≤ − ≤ −}

 

  ,

4 ₁ ₄

4

n− _i _n

 _{ ≤ − ≤ −}

 

  .

Therefore, D Cev

(

n−1, 1i− ≠ Φ

)

, D Cev

(

n−2, 1i− ≠ Φ

)

, D Cev

(

n−3, 1i− ≠ Φ

)

, and D Cev

(

n−4, 1i− ≠ Φ

)

. Theorem 2.7 [5]

For every n≥5 and 4 n i_{≥  } 

 ,

1) If D Cev

(

n−1, 1i− =

)

D Cev

(

n−2, 1i− =

)

D Cev

(

n−3, 1i− = Φ

)

and D Cev

(

n−4, 1i− ≠ Φ

)

then

(

,

) {

{

1, , ,5 3

} {

, 2, , ,6 2

} {

, 3, , ,7 1

} {

, 4, ,8 ,

}

ev n n n n n D C i = e e e− e e e− e e e− e e e .

2) If D Cev

(

n−2, 1i− =

)

D Cev

(

n−3, 1i− =

)

D Cev

(

n−4, 1i− = Φ

)

and D Cev

(

n−1, 1i− ≠ Φ

)

then

(

,

)

{ }

[ ]

ev n n D C i = e .

3) If D Cev

(

n−1, 1i− = Φ

)

,D Cev

(

n−2, 1i− ≠ Φ

)

,D Cev

(

n−3, 1i− ≠ Φ

)

and D Cev

(

n−4, 1i− ≠ Φ

)

then

(

,

)

1 2 3

ev n

D C i =Y Y Y∪ ∪ , where

{

} {

}

{

}

1 1, , ,5 n 5, n1 , 2, , ,6 n 4, n , 3, , ,7 n 3, n1 , 4, , ,8 n 2, n Y = e e e− e− e e e− e e e e− e− e e e− e

{ }

(

)

{ }

(

)

{ }

2 1 2 2 3

2 2 1 2 2 2 3

, if / , 1

, otherwise

n ev n

n

X X

X X

e e D C i

Y e e X D C i

e

− −

  ∈ ∈ − 

  

=  ∈ ∈ − 

 _ 

 

(7)

{ }

(

)

{ }

(

)

{ }

(

)

{ }

3 1 3 3 4

2 2 3 3 4

1 3 3 3

3 3

4

, if / , 1

, otherwise

n ev n

n

X X X X

Y X

e e D C i

e e X X D C i

e

− −

 ∈ ∈ −



∈ ∈ −



 

 

=  

 

 

∈ ∈ −

 

 

∪

4) If D Cev

(

n−3, 1i− = Φ

)

, D Cev

(

n−2, 1i− ≠ Φ

)

, and D Cev

(

n−1, 1i− ≠ Φ

)

then

(

,

)

{

[ ]

{ }

/

[ ]

}

ev n n n D C i = e − x x e∈

5) If D Cev

(

n−1, 1i− ≠ Φ

)

,D Cev

(

n−2, 1i− ≠ Φ

)

,D Cev

(

n−3, 1i− ≠ Φ

)

and D Cev

(

n−4, 1i− ≠ Φ

)

then

(

)

{

{ }

(

)

}

{

{ }

(

)

}

{ }

(

)

{

}

{

{ }

(

)

}

1 1 1 2 1 2 2

3 2 3 3 4 3 4 4

, / , 1 / , 1

/ , 1 / , 1

ev n n ev n n ev n

n ev n n ev n

D C i X e X D C i X e X D C i

X e X D C i X e X D C i

− − −

− − − −

= ∈ − ∈ −

∈ − ∈ −

∪ ∪ ∪

∪ ∪ ∪ ∪

Proof:

1) Since, D Cev

(

n−1, 1i− =

)

D Cev

(

n−2, 1i− =

)

D Cev

(

n−3, 1i− = Φ

)

and D Cev

(

n−4, 1i− ≠ Φ

)

, by Lemma 2.6 (i) 4

n= k, and i k= for some k N∈ . The sets

{

e e1 5, , , en−3

} {

, e e2, , ,6 en−2

} {

, e e3, , ,7 en−1

} {

, , , ,e e4 8 en

}

have

4

n_{elements and each one covers all vertices. Also, no other sets of cardinality} 4

n_{covers all vertices.}

Therefore, the collection of ev-dominating sets of cardinality 4 n_is

{

} {

}

{

e e1, , ,5 en−3 , e e2, , ,6 en−2 , e e3, , ,7 en−1 , e e4, , ,8 en

}

Hence, D C iev

(

n,

) {

=

{

e e1, , ,5 en−3

} {

, e e2, , ,6 en−2

} {

, e e3, , ,7 en−1

} {

, e e4, ,8,en

}

.

2) We have D Cev

(

n−2, 1i− =

)

D Cev

(

n−3, 1i− =

)

D Cev

(

n−4, 1i− = Φ

)

and D Cev

(

n−1, 1i− ≠ Φ

)

. By Lemma 2.6 (2), we have i = n. So, D C iev

(

n,

)

=

{ }

[ ]

en .

3) We have D Cev

(

n−1, 1i− = Φ

)

,D Cev

(

n−2, 1i− ≠ Φ

)

,D Cev

(

n−3, 1i− ≠ Φ

)

and D Cev

(

n−4, 1i− ≠ Φ

)

, by

Lemma 2.6 (3), n=4k+2 and 4 2

4 1

i _ k+ _ k

 =

= + , for some k N∈ .

Let Y1=

{

e e1, , ,5 e4 3k− ,e4 1k+

} {

, e e2, , ,6 e4 2k− ,e4k+2

} {

, e e3, ,7,e4 1k−,e4 1k+

} {

, e e4, , ,8 e e4k, 4k+2

}

{ }

(

)

{

}

(

)

{

}

4 1 2 2 4 1

2 4 1 2 2 2 4 1

4 2 2

, if / ,

, otherwise

k ev k

k

X X X

e e D C k

Y e X k

e

X

e D C

−

+ −

+

  ∈ ∈ 

  

 

=  ∈ ∈ 

  

  

 

∪

{

}

(

)

{ }

(

)

{

}

(

)

{

}

4 1 1 3 3 4 2

4 2 3 3 4 2

4 1 3 3 3 4 2

3 3

4 2

, if / ,

, otherwise

k ev k

k

e e D C k

e e

X X X X

Y X

X D

X C k

e

− −

−

+ −

+

 ∈

 

 

=  

 



∈ 

∈ ∈

 

∈ ∈

 

 

∪

We shall prove that D Cev

(

4k+2,k+ =1

)

Y Y Y1∪ ∪2 3. It is clear that Y1⊆D Cev

(

4 2k+ ,k+1

)

,

(

)

2 ev 4 2k , 1

Y ⊆D C + k+ , and Y3 ⊆D Cev

(

4 2k+ ,k+1

)

. Therefore, Y Y Y1∪ ∪2 3⊆D Cev

(

4 2k+ ,k+1

)

. Conversely, Let Y D C∈ ev

(

4 2k+ ,k+1

)

. Suppose, Y is of the form

{

e e1 5, , , e4 3k− ,e4 1k+

}

,

(8)

1

Y Y∉ and Y is of the form

{ }

(

)

{

}

(

)

{

}

4 1 2 2 4 1

4 1 2 2 2 4

2 1

4 2

, if / ,

, otherwise

k ev k

k

e e D C k

e e X D C

X X X e X k − + − +   ∈ ∈      _∈ _∈            

∪ then Y Y∈ ₂ ⊆D Cev

(

_{4 1}k−,k

)

.

Now suppose, Y Y∉ 1, Y Y∉ 2 and Y∈Dev

(

C4 2k+ ,k+1

)

. We split D Cev

(

4 2k− ,k

)

as four parts. If

(

)

3 ev 4 2k ,

X ∈D C − k with e1∈X3 then X3∪

{

e4 1k−

}

∈Y3 and X3∪

{ }

en−3 ∉Y2 and ∉Y1. If

(

)

3 ev 4 2k ,

{ }

e4k ∈Y3 and X3∪

{ }

e4k ∉Y2 and ∉Y1. If

(

)

3 ev 4 2k ,

{

e4 1k+

}

∈Y3 and X3∪

{

e4 1k+

}

∉Y2 and ∉Y1. If

(

)

3 ev 4 2k ,

{

e4 2k+

}

∈Y3 and X3∪

{

e4 2k+

}

∉Y2 and ∉Y1. In this case Y is of

the form

{

}

(

)

{ }

(

)

{

}

(

)

{

}

4 1 1 3 3 4 2

4 2 3 3 4 2

4 1 3 3 3 4

3

2

4 2

, if / ,

, otherwise

k ev k

k

X X X X

e e D C k

e e X D C k

e X X − − − + − +  ∈ ∈  ∈ ∈   ∈ ∈   

∪ then Y Y∈ ∈3 D Cev

(

4 2k− ,k

)

. Therefore,

(

4 2, 1

)

1 2 3 ev k

D C + k+ ⊆Y Y Y∪ ∪ . Thus, we have proved that

(

,

)

1 2 3

ev n

D C i =Y Y∪ ∪∪Y

where Y₁=

{

e e₁, , ,₅ en−₅,en−₁

} {

, e e₂, , ,₆ en−₄,en

} {

, e e₃, , ,₇ en−₃,en−₁

} {

, e e₄, , ,₈ en−₂,en

}

{ }

(

)

{ }

(

)

{ }

2 1 2 2 3

2 2 1 2 2 2 3

, if / , 1

, otherwise

n ev n

n

e e D C i

Y e e

X X

X X X D C i

e − − − −   ∈ ∈ −       =_ _ ∈ ∈ − _         ∪

{ }

(

)

{ }

(

)

{ }

(

)

{ }

3 1 3 3 4

2 2 3 3 4

1 3 3 3

3 3

4

, if / , 1

, otherwise

n ev n

n

X X X X

Y X

e e D C i

e e X X D C i

e − − − − − −  ∈ ∈ −  ∈ ∈ −        =         ∈ ∈ −     ∪ .

4) If D Cev

(

n−3, 1i− = Φ

)

,D Cev

(

n−2, 1i− ≠ Φ

)

, and D Cev

(

n−1, 1i− ≠ Φ

)

, by Lemma 3.6 (iv) i n= −1. Therefore D C iev

(

n,

)

=

{

[ ]

en −

{ }

x x e/ ∈

[ ]

n

}

.

5) D Cev

(

n−₁, 1i− ≠ Φ

)

,D Cev

(

n−₂, 1i− ≠ Φ

)

,D Cev

(

n−₃, 1i− ≠ Φ

)

and D Cev

(

n−₄, 1i− ≠ Φ

)

.

Clearly,

{

{ }

(

)

}

{

{ }

(

)

}

{ }

(

)

{

}

{

{ }

(

)

}

(

)

1 1 1 2 1 2 2

3 2 3 3 4 3 4 4

/ , 1 / , 1

/ , 1 / , 1 , .

n ev n n ev n

n ev n n ev n ev n

X e X D C i X e X D C i D C i

− − − − − − − ∈ − ∈ − ∈ − ∈ − ⊆ ∪ ∪ ∪ ∪ ∪ ∪ ∪

Conversely, let Y D C i∈ ev

(

n,

)

. Then en or en−1 or en−2 or en−3∈Y . If en∈Y , then we can write

{ }

1 n

Y X= ∪ e , for some X1∈D Cev

(

n−1, 1i−

)

. If en−1∈Y and en∉Y then we can write Y X= 2∪

{ }

en−1 , for some X2∈D Cev

(

n−2, 1i−

)

. If en−2∈Y and en∉Y e, n−1∉Y then we can write Y X= 3∪

{ }

en−2 , for some

(

)

3 ev n3, 1

X ∈D C− i− . If en−3∈Y, en∉Y e, n−1∉Y , en−3∉Y then we can write Y X= 4∪

{ }

en−3 , for some

(

)

4 ev n1, 1 X ∈D C− i− .

Therefore we proved that

(

)

{

{ }

(

)

}

{

{ }

(

)

}

{ }

(

)

{

1 3 2 1 3 1 3

}

2

{

4 1

{ }

32 4

(

2 4

)

}

, / , 1 / , 1

/ , 1 / , 1 .

ev n n ev n n ev n

n ev n n ev n

(9)

Hence,

(

)

{

{ }

(

)

}

{

{ }

(

)

}

{ }

(

)

{

}

{

{ }

(

)

}

1 1 1 2 1 2 2

3 2 3 3 4 3 4 4

, / , 1 / , 1

/ , 1 / , 1

ev n n ev n n ev n

n ev n n ev n

− − −

− − − −

= ∈ − ∈ −

∈ − ∈ −

∪ ∪ ∪

∪ ∪ ∪ ∪

3. Edge-Vertex Domination Polynomials of Cycles

Let

(

)

(

)

4

, n , i

ev n _i n ev n

D C x _{ }d C i x

= _{ }

=

∑

be the ev-domination polynomial of a cycle Cn. In this section, we de-rive the expression for D C xev

(

n,

)

.

Theorem 3.1 [6]

1) If D C iev

(

n,

)

is the family of ev-dominating sets with cardinality i of Cn, then

(

,

)

(

1, 1

)

(

2, 1

)

(

3, 1

)

(

4, 1

)

ev n ev n ev n ev n ev n

d C i =d C i− − +d C − i− +d C− i− +d C − i− where d C iev

(

n,

)

= D C iev

(

n,

)

.

2) For every n≥5,

(

,

)

(

1,

)

(

2,

)

(

3,

)

(

4,

)

ev n ev n ev n ev n ev n D C x =x D C − x +D C− x +D C − x D C+ − x  with the initial values

(

1,

)

ev

D C x =x,

(

)

2

2, 2

ev

D C x = x +x,

(

)

3 2

3, 3 3

ev

D C x = x + x +x,

(

)

4 3 2

4, 4 6 4

ev

D C x = x + x + x +x. Proof:

1) Using (1), (2), (3), (4) and (5) of Theorem 2.7, we prove (1) part.

Suppose, D Cev

(

n−1, 1i− =

)

D Cev

(

n−2, 1i− =

)

D Cev

(

n−3, 1i− = Φ

)

and D Cev

(

n−4, 1i− ≠ Φ

)

then,

(

,

) {

{

1, ,5 , 3

} {

, 2, , ,6 2

} {

, , , ,3 7 1

} {

, 4, ,8 ,

}

ev n n n n n D C i = e e e− e e e− e e e− e e e .

Therefore, D C iev

(

n,

)

=

{

e₁, , ,e₅ en−₃

} {

, e e₂, ,₆,en−₂

} {

, e e₃, , ,₇ en−₁

} {

, e e₄, ,₈,en

}

=4. In this case

(

4, 1

)

{

1, ,5 , 3

} {

, 2, ,6 , 2

} {

, 3, , ,7 1

} {

, 4, , ,8

}

4

ev n n n n n

D C − i− = e e e− e e e− e e e− e e e = and

(

1, 1

)

(

2, 1

)

(

3, 1

)

0 ev n ev n ev n

D C − i− = D C − i− = D C− i− = . Therefore, in this case the theorem holds. Suppose, D Cev

(

n−2, 1i− =

)

D Cev

(

n−3, 1i− =

)

D C

(

n−4, 1i− = Φ

)

and D Cev

(

n−1, 1i− ≠ Φ

)

, then

(

,

)

{ }

[ ]

ev n n

D C i = e Therefore, D C i_ev

(

_n,

)

=

{ }

[ ]

e_n =1. In this case D Cev

(

n−₁, 1i− =

)

{

[ ]

en−₁

}

. Therefore,

(

1, 1

)

{

[ ]

1

}

1

ev n n

D C − i− = e− = and D Cev

(

n−2, 1i−

)

= D Cev

(

n−3, 1i−

)

= D Cev

(

n−4, 1i−

)

=0. Therefore, in this case the theorem holds.

Suppose,

(

)

(

)

(

2

)

(

2

)

1, 1 , 2, 1 , 3, 1 and 4, 1

ev n ev n n n

D C − i− = Φ D C − i− ≠ Φ D C − i− ≠ Φ D C− i− ≠ Φ. In this case,

(

,

)

1 2 3

ev n

D C i =Y Y Y∪ ∪ where

{

} {

}

{

}

1 1, , ,5 n 5, n1 , 2, , ,6 n 4, n , 3, , ,7 n 3, n1 , 4, , ,8 n 2, n Y = e e e− e− e e e− e e e e− e− e e e− e

{ }

(

)

{ }

(

)

{ }

2 2 2 2

2 2 1 2 2 2

, if 1 / , 1

, if 2 / , 1

, otherwise

n ev n

n

e D C i

Y e X D C

X X

X X i

e

− −

  ∈ ∈ − 

  

=  ∈ ∈ − 

  



 

(10)

{ }

(

)

{ }

(

)

{ }

(

)

{ }

3 3 3 3

2 3 3 3

1 3 3

3 3

3

, if 1 / , 1

, if 2 / , 1

, if 3 / , 1

, otherwise

n ev n

n

e D C i

e

X X X X Y

D

X X C

e X

i

− −

 ∈ ∈ −



 

 

=  

 



∈ ∈ −

 

∈ ∈ −

 

 

∪

(

n,

)

= +4 D Cev

(

n−3, 1i− +

)

D Cev

(

n−4, 1i−

)

. Also, D Cev

(

n−1, 1i−

)

=0 and

(

2, 1

)

4

ev n

D C − i− = . Therefore, D C iev

(

n,

)

= D Cev

(

n−1, 1i− +

)

D Cev

(

n−3, 1i− +

)

D Cev

(

n−4, 1i−

)

and

(

1, 1

)

0

ev n

D C − i− = . Therefore, in this case the theorem holds. Suppose,

(

1, 1

)

,

(

2, 1

)

and

(

3, 1

)

ev n ev n ev n

D C− i− ≠ Φ D C− i− ≠ Φ D C− i− = Φ Then we have D C iev

(

n,

)

=

{

[ ]

en −

{ }

x x e/ ∈

[ ]

n

}

.

(

n,

)

=n. In this case, D Cev

(

n−1, 1i−

)

= −n 1, D Cev

(

n−2, 1i−

)

=1 and

(

3, 1

)

0

ev n

D C− i− = . Therefore,

(

,

)

(

1, 1

)

(

2, 1

)

(

3, 1

)

1 1 0

ev n ev n ev n ev n

D C i = D C − i− + D C − i− +D C − i− = − + + =n n. Therefore, in this case the theorem holds.

Suppose,

(

)

(

)

(

2

)

(

)

1, 1 , , 12 , , 13 and , 14

ev n ev n n ev n

D C− i− ≠ Φ D C− i− ≠ Φ D C− i− ≠ Φ D C − i− ≠ Φ. In this case, we have

(

)

{

{ }

(

)

}

{

{ }

(

)

}

{ }

(

)

{

}

{

{ }

(

)

}

1 1 1 2 1 2 2

3 2 3 3 4 3 4 4

, / , 1 / , 1

/ , 1 / , 1 .

ev n n ev n n ev n

n ev n n ev n

− − −

− − − −

= ∈ − ∈ −

∈ − ∈ −

∪ ∪ ∪

∪ ∪ ∪ ∪

Therefore,

(

,

)

(

1, 1

)

(

2, 1

)

(

3, 1

)

(

4, 1 .

)

ev n ev n ev n ev n ev n D C i = D C− i− +D C − i− + D C− i− +D C − i− Hence,

(

,

)

(

1, 1

)

(

2, 1

)

(

3, 1

)

(

4, 1 .

)

d C i =d C i− − +d C− i− +d C − i− +d C− i−

(

,

)

i

(

1, 1

)

i

(

2, 1

)

i

(

3, 1

)

i

(

4, 1

)

i

d C i x =d C − i− x d C+ − i− x d C+ − i− x d C+ − i− x

(

,

)

i

(

1, 1

)

i

(

2, 1

)

i

(

3, 1

)

i

(

4, 1

)

i

d C i x d C − i x d C − i x d C− i x d C− i x

∑ = ∑ − + ∑ − + ∑ − + ∑ −

(

)

(

)

(

)

(

)

(

)

1 1

1 2

1 1

3 4

, , 1 , 1

, 1 , 1

i i i

ev n ev n ev n

i i ev n ev n

d C i x x d C i x x d C i x x d C i x x d C i x

− −

∑ = ∑ − + ∑ −

+ ∑ − + ∑ −

(

)

(

)

1

(

)

1

(

)

1

(

)

1

1 2 3 4

, i , 1 i , 1 i , 1 i , 1 i

d C i x x d C i x− d C i x− d C i x− d C i x−

− − − −

 

∑ = _∑ − + ∑ − + ∑ − + ∑ − _

(

,

)

(

1,

)

(

2,

)

(

3,

)

(

4,

)

ev n ev n ev n ev n ev n D C x =x D C − x +D C− x +D C − x D C+ − x . with the initial values

(

1,

)

ev

D C x =x

(

)

2

2, 2

ev

D C x = x +x

(

)

3 2

3, 3 3

ev

D C x = x + x +x

(

)

4 3 2

4, 4 6 4

ev

(11)

We obtain d C i_ev

(

_n,

)

for 1 ≤n ≤ 16 as shown in Table 1.

In the following Theorem, we obtain some properties of d C iev

(

n,

)

.

Theorem 3.2

The following properties hold for the coefficients of D C xev

(

n,

)

; 1) d C nev

(

4n,

)

=4, for every n∈ N.

2) d C nev

(

n,

)

=1, for every n∈ N.

3) d C n_ev

(

_n, − =1

)

n, for every n ≥ 2.

4)

(

)

2

(

)

1

, 2

2 ev n

n n

d C n− =nC = − , for every n≥ 3.

5)

(

)

3

(

)(

)

1 2

, 3

6 ev n

n n n

d C n− =nC = − − , for every n≥ 4.

6)

(

)

4

(

)(

)

1 2 3

, 4

4! ev n

n n n n

d C n− =nC n− = − − − −n, for every n≥ 5.

7) d Cev

(

4 1n−,n

)

=4 1n− , for every n∈ N.

Proof:

1) Since D C nev

(

4n,

) {

=

{

e e1, , ,5 en−3

} {

, e e2, , ,6 en−2

} {

, e e3, , ,7 en−1

} {

, e e4, ,8,en

}

, we have

(

4 ,

)

4

ev n

d C n = .

2) Since D C nev

(

n,

)

=

{ }

[ ]

en , we have the result d C iev

(

n,

)

=1 for every n∈ N. 3) Since Dev

(

Cn,n− =1

)

{

[ ]

en −

{ }

x /x∈

[ ]

en

}

, we have d C nev

(

n, − =1

)

n for n ≥ 2.

4) By induction on n. The result is true for n=3. L.H.S.=d Cev

(

3,1 3

)

= (from Table 1) R.H.S. 3 2₂ 3

×

= = .

[image:11.595.91.539.457.722.2]

Therefore, the result is true for n = 3. Now suppose that the result is true for all numbers less than ‘n’ and we prove it for n. By Theorem 3.1

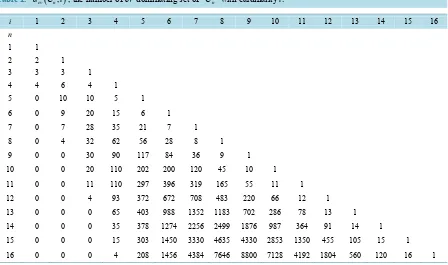
Table 1. d C iev

(

n,

)

, the number of ev-dominating set of Cn with cardinality i.

i 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

n

1 1

2 2 1

3 3 3 1

4 4 6 4 1

5 0 10 10 5 1

6 0 9 20 15 6 1

7 0 7 28 35 21 7 1

8 0 4 32 62 56 28 8 1

9 0 0 30 90 117 84 36 9 1

10 0 0 20 110 202 200 120 45 10 1

11 0 0 11 110 297 396 319 165 55 11 1

12 0 0 4 93 372 672 708 483 220 66 12 1

13 0 0 0 65 403 988 1352 1183 702 286 78 13 1

14 0 0 0 35 378 1274 2256 2499 1876 987 364 91 14 1

15 0 0 0 15 303 1450 3330 4635 4330 2853 1350 455 105 15 1

(12)

(

)

(

)

(

)

(

)

(

)

(

)(

1

_{) ( ) ( )( ) ( )}

2 3

₍

4

₎₍

₎

₍

₎

, 2 , 3 , 3 , 3 , 3

1 2 ₁ 1 ₁ _{2 2} ₁ 1 ₁ _{2 2} 1 ₁

2 2 2 2

d C n d C n d C n d C n d C n

n n

n n n n n n n n

− − − −

− = − + − + − + −

− −

= + − = _ − − + − _= _ − − + _= _ − _

5) By induction on n, the result is true for n=4. L.H.S.=d Cev

(

4,1

)

=4 (from Table 1).

(

4

)

4.3.2

R.H.S. ,1 4

6 ev

d C

= = = . Therefore, the result is true for n=4. Now suppose the result is true for all

natural numbers less than n. By Theorem 3.1,

(

)

(

)

(

)

(

)

(

)

(

)(

) (

)(

_{) ( )}

(

)(

) (

)(

) (

)

(

_{) ( )( ) ( )}

(

_{) ( )( ) ( )}

(

)(

)

_[

_]

(

)(

)

1 2 3 4

, 3 , 4 , 4 , 4 , 4

1 2 3 2 3

2

6 2

1 ₁ ₂ _{3 3} ₂ _{3 6} ₂

6 2

1 3 3 3 6

6 2

1 3 3 1

6

2 1 2 1

3 3

6 6

n n n n n

n

n n n n n n

n

n n n

n

n n n

n n n n n

n

− − − −

− = − + − + − + −

− − − − −

= + + −

= _ − − − + − − + − _

−

= _ − − + − + _

−

= _ − − + − _

− − − −

= − + =

6) By induction on n, the result is true for n = 5. L.H.S.=d Cev

(

₅,1

)

=0 (from Table 1)

(

1

)(

2

)(

3

)

5 4 3 2

R.H.S. 5 0

1 2 3 4 1 2 3 4

n n n n

n

− − − × × ×

= − = − =

× × × × × ×

Therefore the result is true for n=5.

Now suppose that the result is true for all natural numbers less than n and we prove it for n. By Theorem 3.1,

(

)

(

)

(

)

(

)

(

)

(

)(

_{) ( ) ( )( )( ) ( )( ) ( )}

(

)(

) (

)(

)

(

)(

)

(

)

(

)(

) (

)(

)

(

)(

)

(

)

1 2 3 4

, 4 , 5 , 5 , 5 , 5

1 2 3 4 2 3 4 3 4

1 4

24 6 2

1 ₁ ₂ ₃ _{4 4} ₂ ₃ _{4 12} ₃ _{4 24} _{4 24}

24

1 ₁ ₂ ₃ _{4 4} ₂ ₃ _{4 12} ₃ _{4 24} _{4 1}

24

n n n n n n n n n

n n

n n n n n n n n n n n

− − − −

− = − + − + − + −

− − − − − − − − −

= − − + + + −

= _ − − − − + − − − + − − + − + _−

(

)(

) (

)(

)

(

)(

)

(

)

(

_{) ( )( )( ) ( )( ) (}

₎

(

)(

_{) ( )( ) ( )}

(

)(

_{) ( )( ) (}

₎

(

)(

)

_[

_]

(

)(

)

1 ₁ ₂ ₃ _{4 4} ₂ ₃ _{4 12} ₃ _{4 24} ₃

24 3

1 2 4 4 2 4 12 4 2

24

3 2

1 4 4 4 12

24

3 2

1 4 4 4 3

24

1 2 3

4 4 24

1 2 3

24

n n n n n n n n n n n

n

n n n n n n n

n n

n n n n

n n

n n n n

n n n

n n

n n n n n

= _ − − − − + − − − + − − + − _−

−

= _ − − − + − − + − + _−

− −

= _ − − + − + _−

− −

= _ − − + − + _−

− − −

= − + −

− − −

= −