R E S E A R C H
Open Access
Diffusive induced global dynamics and
bifurcation in a predator-prey system
Nadia N Li
**Correspondence:
lina3718@163.com
Department of Mathematics and Statistics, Zhoukou Normal University, Zhoukou, Henan 466001, China
Abstract
In this paper, a diffusive Leslie-type predator-prey model is investigated. The existence of a global positive solution, persistence, stability of the equilibria and Hopf
bifurcation are studied respectively. By calculating the normal form on the center manifold, the formulas determining the direction and the stability of Hopf bifurcations are explicitly derived. Finally, our theoretical results are illustrated by a model with homogeneous kernels and one-dimensional spatial domain.
Keywords: existence of a global positive solution; global stability; permanence; Lyapunov function; Hopf bifurcation
1 Introduction
Bifurcation phenomena are observed and studied in a variety of fields, such as engineering [], ecological [], chemical [], biological [–], control [, ] and neural networks [–]. A classical predator-prey model is investigated as follows:
⎧ ⎨ ⎩
˙
x(t) =x( –x) – axx+bxy+,
˙
y(t) =y(δ–βyx).
(.)
The study shows that model (.) has complex bifurcation phenomena and dynamic be-havior, such as the existence of both Hopf bifurcation and Bogdanov-Takens bifurcation. For more detailed results on model (.), one can refer to [].
As we all know, the spatial heterogeneity of predator and prey distributions is more or less obvious. The predator or prey can flow from higher density regions to lower density ones, which is called normal diffusion. And specifically, to the best of our awareness, few papers which discuss the dynamic behavior of model (.) with diffusion have appeared in the literature. This paper attempts to fill this gap in the literature. To achieve this goal, we look at the following model:
⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩
∂u
∂t =du+u( –u) – uv
au+bu+, (x,t)∈(,lπ)×[,∞),t> , ∂v
∂t =dv+v(δ– βv
u), (x,t)∈(,lπ)×[,∞),t> ,
ux(t, ) =vx(t, ) = ,
ux(t,lπ) =vx(t,lπ) = , t> ,
u(,x) =u(x)≥, v(,x) =v(x)≥, x∈[,lπ],
(.)
whereui=ui(x,t),i= , ,= ∂
∂x denotes the Laplacian operator,d,dare diffusion
coef-ficients of prey and predator, respectively.is a bounded subset with sufficiently smooth boundary∂inRn, whereRnis an arbitrary positive-integerN-dimensional space.is
the Laplacian operator in the region. The no-flux boundary condition means that the statical environmentis isolated.
In the biological field, the study of the stability and bifurcations of the reaction-diffusion models describing a variety of biological phenomena is one of the fundamental problems, which can be conducive to understand the dynamic behavior. Recently, the stability of the steady state [, ] and that of the non-constant steady state solution [–] are investi-gated. The main contributions of this article are as follows: (a) the existence of the global positive solution and the persistence of system (.) are discussed in detail; (b) the Hopf bifurcation analysis of system (.) is provided; (c) the Lyapunov function is constructed to complete the proof of global stability of the equilibria.
The rest of this article is organized as follows. In Section , the existence of a global pos-itive solution of (.) as well as the boundedness are considered. In Section , the persis-tence of the system is investigated. In Section , the stability of the constant equilibria, the existence of Hopf bifurcations and the stability of a bifurcating periodic solution around the interior constant equilibrium are investigated. In Section , the global stability of the constant equilibria is proved by the Lyapunov function method under certain conditions investigated. Finally, simulations are presented to verify our theoretical analysis.
2 Existence of a global positive solution of (1.2)
For convenience, we introduce some notations. Forx,y∈R, we denotex∧y:min{x,y},x∨ y:=max{x,y},x+:x∨,x–: (–x)∨ and extend these notations to real-valued functions.
If (∨,≥) is a partially ordered vector space, we denote its positive cone by∨+:={v∈ ∨:
v≥}. Forp∈[, +∞),p>N/, letX={Lp()}. AssumeW= (u,v)∈X, and its norm is defined asW=up+vp. Now, model (.) can be rewritten as an abstract differential
equation
⎧ ⎨ ⎩ dz
dt =Az+H(z), t∈(,∞),
z() =z,
(.)
wherez= (u(x,t),v(x,t))T,z
= (u,v)T,
A=
–I
–I
, (.)
with
D(A) =
(u,v)∈ C(¯),∂u
∂ν
∂
= ∂v
∂ν
∂
=
and
H(z) =
u( –u–auuv+bu+)
v(δ+ –βvu)
Next, we prove the existence of the local solution for (.). First, we give out the following lemma.
Lemma . For every z∈X+,the Cauchy problem(.)has a unique maximal local
so-lution
z∈[,Tmax);X
∩C(,Tmax);X
∩C(,Tmax);D(A)
, (.)
which satisfies the following Duhamel formula for t∈[,Tmax):
z(t) =etApz
+ t
e(t–s)ApHz(s)ds, (.)
where Ap is an operator and the closure of A in X. Moreover, if Tmax < ∞, then
lim supT–
maxz(t)=∞.
Proof Since the operatorApis the closure ofAinX, it generates an analytic, condensed,
strong continuous operator semi-groupetAp. Furthermore, fort> , we have
etApw≤e–tw, ∀w∈X. (.)
Moreover, we observe thatH:D(A)→Xis locally Lipschitz on a bounded set. Via
Theo-rem .. in [], we complete his proof.
Lemma . For the initial-boundary problem of model(.),the components of its solution u(x,t),v(x,t)are nonnegative.
Proof To proveu(x,t),v(x,t)≥,
⎧ ⎨ ⎩
∂u
∂t =du+u+( –u+– u+v+ au++bu++
),
∂v
∂t =dv+cv+(δ– βv+
u+ ),
(.)
with the boundary and initial conditions
⎧ ⎨ ⎩
∂u ∂ν|=
∂v ∂ν|= ,
u(x, ) =u, v(x, ) =v.
After multiplying (.) byu–andv–, respectively, and integrating by parts on the domain
, we obtain
⎧ ⎨ ⎩
–dtd|∂u–|dx–d
|∇∂u–|dx= ,
–dtd|∂v–| dx–d
|∇∂v–|dx= .
Hence, fort∈(,Tmax),
u–(·,t)+v–(·,t)≤u–(·, )+v–(·, )= .
Consequently,u(x,t)≥,v(x,t)≥.
of the positive solution for (.). Via Lemmas . and ., we only need to show that the solution of model (.) is uniformly bounded, i.e., dissipation. For this, we first introduce
the following lemma.
Lemma .([]) Suppose that z(x,t)satisfies the following equation:
⎧ ⎪ ⎪ ⎨ ⎪ ⎪ ⎩ ∂z
∂t=dz+z( –z), x∈,t> , ∂z
∂n= , x∈,t> ,
z(x, ) =z(x)≥,≡, x∈.
Thenlimt→∞z(x,t) = for any x∈.
Theorem . The solution(u(x,t),v(x,t))of(.)satisfies the following inequalities:
lim sup
t→∞ maxx∈u(x,t)≤, lim supt→∞ maxx∈v(x,t)≤ δ β.
Proof
⎧ ⎪ ⎪ ⎨ ⎪ ⎪ ⎩
∂u
∂t ≤du+u( –u), x∈,t> , ∂u
∂n= , x∈,t> ,
u(x, ) =u(x), x∈.
By the comparison principle and Lemma ., we obtain easily the first inequality. There-fore, there existT> and sufficiently small <≤ such thatu(x,t)≤ +for anyx∈
andt>T. For the second equation, we have the following inequality: ⎧
⎪ ⎪ ⎨ ⎪ ⎪ ⎩ ∂v
∂t ≤dv+v(δ– βv
+), x∈,t> , ∂v
∂n= , x∈,t> ,
v(x, ) =v(x), x∈.
By the comparison principle, for the above <≤, there existsT(>T) such that, for
anyt>T,
v(x,t)≤δ( +)
β +.
For the arbitrariness of> , we obtain
lim sup
t→∞ maxx∈v(x,t)≤ δ
β, ∀x∈.
As a result, we complete this proof. By Lemmas ., . and Theorem ., we can get the
following theorem.
Theorem . System (.) has a unique, nonnegative and bounded solution Z(x,t) = (u(x,t),v(x,t))such that
3 Permanence
In this section, we show that any nonnegative solution (u(x,t),v(x,t)) of (.) lies in a cer-tain bounded region ast→ ∞for allx∈.
We make the following hypothesis: (H)bβδ < .
Theorem . If(H)holds,the solution(u,v)of(.)satisfies the following inequalities:
lim inf
t→∞ minx∈u(x,t)≥ – δ
bβ, lim inft→∞ minx∈v(x,t)≥ δ( – δ
bβ)
β .
Proof From the first equation of (.) and Theorem ., we have
∂u
∂t ≥du+u
–u–
δ(+) β +
b
.
By the comparison principle and Lemma ., we obtain easily
lim inf
t→∞ minx∈u(x,t)≥ – δ
bβ.
From the second equation of (.), we have
∂v
∂t≥dv+v
δ– βv
–bβδ
.
This implies
lim inf
t→∞ minx∈v(x,t)≥
δ( –aβδ )
β .
From Theorems . and ., we can easily obtain the following theorem.
Theorem . If(H)holds,model(.)is permanent.
4 The stability of equilibria and the existence of Hopf bifurcations
4.1 The existence of equilibrium of model (1.2)
The system has always constant equilibriaE(, ). By the direct calculation, there exists
a unique constant positive equilibrium denoted byE∗(u,v) if and only if the following
cubic equation
au+
δ β +b–a
u+ ( –b)u– = (.)
holds in the interval (, ). Note that the third-order algebraic equation (.) can have one, two, or three positive roots in the interval (, ) which can be evaluated by using the root formula of the third-order algebraic equation. Correspondingly, system (.) can have one, two, or three positive equilibria. Regarding the number of positive equilibria in the interval (, ) of (.), [] gives the result in detail as follows.
Lemma .([]) Let = (βδ +b–a)+ a(b– )and= – + (a+ a( –b)(δ β+
(H) If> ,then model(.)has a unique positive equilibriumE∗,which is an elementary and anti-saddle equilibrium.
(H) If= and > ,then the model has two different positive equilibria:an elementary anti-saddle equilibriumE∗and a degenerate equilibriumE.
(H) If= and = ,the model has a unique positive equilibriumE(–b,β(–δb)), which is a degenerate equilibrium.
(H) If< ,βδ =a–b–√a( –b)and–√a<b< ,then model(.)has three different positive equilibriaE∗,E∗andE∗,which are all elementary equilibria and
E∗is a saddle.
Remark We further consider the following condition (H). We suppose (H) is satisfied throughout the rest of this paper.
4.2 The existence of Hopf bifurcation
In this section we assume that (H) holds. We first assume thatE∗(u,v) is any point of
system (.). Now we define the real-valued Sobolev space
X:= (u,v)∈H(,lπ): (ux,vx)|x=,lπ=
,
and the complexification ofX
XC:=X⊕iX={x+ix:x,x∈X}.
The linearized system of (.) at any pointE(u,v) has the form
L=
A –B
δ β –δ
(.)
with the domainDL(s)=XC, where
A= – u–
uv(bu+ )
(au+bu+ )
, B= u
au+bu+
.
Obviously,B> . From Wu [], we obtain that the characteristic equation of (.) is
λy–dy–Leλy= , y∈dom(d),y= . (.)
It is well known that the eigenvalue problem
–ϕ=μϕ, x∈(,lπ) :ϕ() =ϕ(lπ) =
has eigenvaluesμn=n
l (n= , , , . . .) with corresponding eigenfunctions
ϕ(x)n=cos
nπ
l , n= , , . . . .
Substituting
y=
∞
k=
yn
yn
cosnπ
into the characteristic Eq. (.), we have
A–dnl –B δ
β –δ– dn
l
yn
yn
=λ
yn
yn
, n= , , , . . . .
Therefore the characteristic Eq. (.) is equivalent to
det(λI–Mn–L) = , (.)
whereIis the × identity matrix andMn=n
l diag{d,d},n= , , , . . . . It follows from
(.) that the characteristic equations for the equilibrium (u,v) are the following
se-quence of quadratic transcendental equations:
n(λ,τ) =λ–Tnλ+Dn= , (.)
where
⎧ ⎨ ⎩
Tn= –(d+d)n
l –δ+A,
Dn=ddn
l + (dδ–dA)n
l +δ(Bδβ –A).
(.)
The eigenvalues are given by
λ,=
Tn±
T n– Dn
, n= , , , . . . . (.)
We make the following hypothesis with fixingδ:
(H) A<ρδ and (H)
Bδ β <A<
d
d δ,
whereρ=min{,dd,Bβ}.
Lemma .
(i) Suppose(H)and(H)are satisfied.Then all the roots of Eq. (.)have a negative real part.
(ii) Suppose(H)and(H)hold,then Eq. (.)has at least one positive real part.
Proof
(i) Obviously, by(H)Tn< forn= , , , . . ., we know all the roots of Eq. (.) have
negative real parts.
(ii) If(H)holds, we know thatDnis monotone increasing with regard ton, and
limn→∞Dn=∞andD< . There exists an integern∗≥such thatDn< when
n= , , , . . . ,n∗. Hence, there areDn< ,Tn– Dn>Tn,λ> andλ< for
n= , , , . . . ,n∗andDn> ,Tn– Dn<Tn,λ> andλ> forn≥n∗. These
complete the proof of (i) and (ii).
From the discussion, we have the following theorem.
Theorem .
(ii) Suppose(H)and(H)hold,the equilibriumE∗is unstable.
Next,we consider the occurrence of Hopf bifurcation of E∗by regarding A as a bifurcation parameter with fixingδ.In the light of(.),it is known that(.)has purely imaginary roots if and only if
A=An= (d+d)
n
l +δ, n= , , . . . , (.)
and Dn> holds.From(.)we know that Anis monotone increasing with regard to n,and
lim
n→∞An=∞, and A=δ> .
Hence,there is An> for n= , , , . . . .Bringing Aninto Dn,we get
Dn= –
dn
l –
dn
l δ+
B
β –
δ. (.)
If D=δ(Bβ– ) > holds,then there exists an integer n∗ ≥such that Dn> when n=
, , , . . . ,n∗and Dn≤when n≥n∗.
Let n∗= [n∗]and={An∗–>An∗–>An∗–>· · ·>A}.
Lemma . IfBβ– > is satisfied,then Eq. (.)has purely imaginary roots if and only if A∈.
Proof Letλn(A) =αn(A) +iωn(A),n= , , . . . ,n∗be the roots of Eq. (.) satisfyingαn(A) = ,ωn(A) =
√
Dn(A). IfβB– > holds, we know thatDnis monotone decreasing with regard
ton, andlimn→∞Dn= –∞andD> . There exists an integern∗ ≥ such thatDn>
whenn= , , , . . . ,n∗. These complete the proof of Lemma .. From expression (.) we
have the following conclusion.
Lemma . Suppose Bβ – > is satisfied, then all the roots of Eq. (.)with A=An
(n→ ∞) have at least one root with a positive real part except the imaginary roots ±i√Dn(An),n∈(, , . . . ,n∗).
Proof If Bβ – > holds, we know thatDnis monotone decreasing with regard ton, and
limn→∞Dn= –∞. Hence, there areDn< ,Tn– Dn>Tn,λ> andλ< forn>n∗. In
combination with Lemma ., we complete the proof of Lemma ..
Based on the above analysis, we have the following theorem.
Theorem . SupposeβB– > is satisfied.Then model(.)undergoes a Hopf bifurcation at the origin when A=Anfor≤n≤n∗.Moreover:
(i) The bifurcation periodic solution fromA=Ais spatially homogeneous,which coincides with the periodic solution of the corresponding ODE system.
(ii) The bifurcation periodic solution fromA=Anis spatially non-homogeneous for
4.3 Direction and stability of Hopf bifurcation
From the previous section, we know that model (.) undergoes a Hopf bifurcation at the origin whenA=An,n= , , . . . ,n∗, wheren∗andAnare defined as in (.).
In this section, we study the direction of Hopf bifurcation and the stability of the bifur-cating periodic solution by applying the center manifold theorem and the normal form theorem of partial differential equations. We first transformE∗of (.) to the origin via the translation:uˆ=u–u,vˆ–vand drop the hats for simplicity of notation, then (.) is
The straightforward computation yields
So
Then we have
and
H=
c
d
–q∗,Qqq a
b
–q∗,Qqq a
b
= ,
H=
e
f
–q∗,Qq¯q a
b
–q∗,Qq¯q a
b
= ,
which impliesW=W= , that is to say,
q∗,Q(W,q)
=q∗,Q(W,q¯)
= .
Therefore
⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩
c(A) ={iωq∗,Qqq · q∗,Qq¯q+q∗,Qqq¯q},
Re(c(A)) =Re{iωq∗,Qqq · q∗,Qq¯q+
q∗,Qqqq¯},
Im(c(A)) =Im{iωq∗,Qqq · q∗,Qq¯q+q∗,Qqqq¯},
T= [Im(c(A)) –Reα(c(δ(δ)))ω (δ
)],
whereω(A) = > , then we have the following theorem.
Theorem . SupposeBβ– > is satisfied.
The Hopf bifurcation at A=Ais backward(resp.forward);
The bifurcation periodic solution from A=Ais asymptotically stable(resp.unstable)if
Re(c(A)) < (resp. > );
The bifurcation periodic solution from A=Ais increasing(resp.decreasing)if T>
(resp. < ).
When <j≤n∗, forAj, we have the following theorem.
Theorem . SupposeβB– > is satisfied.
The Hopf bifurcation at A=Ajfor <j≤n∗is backward(resp.forward);
The bifurcation periodic solution from A=Ajis asymptotically stable(resp.unstable)if
Re(c(Aj)) < (resp. > );
The bifurcation periodic solution from A=Ajis increasing(resp.decreasing)if T>
(resp. < )for <j≤n∗,whereRe(c(Aj))is defined in Appendix.
5 Global stability of equilibria
In this section, we continue to study the global stability of equilibria.
Theorem . Suppose that the hypothesis of Lemma.holds,then the positive constant equilibrium E∗(u,v)is globally asymptotically stable if
auv
Qp∗ – v
[a+b+ ]p∗ < , (.a)
–bβδ +
v
( –bβδ )Qp∗–
δ
β( – δ bβ)
–uv
δ
( – δ bβ)β
–
b > , (.c)
where Q= [a( –bβδ )+b( –bβδ ) + ].
Proof Let (u(x,t),v(x,t)) be any solution of model (.). We introduce the Lyapunov func-tion
V(u,v) =
u–u–ln
u u
+
β
v–v–ln
v v
dx.
Now, we take the derivative ofV with regard totalong the trajectory of model (.). Then
˙
V=V+V,
where
V =d
–u u
u dx+d
β
–v v
v dx
≤–
du|∇u|
u +
dv|∇v| βv
dx≤
and
V=
(u–u)
–u– uv au+bu+
dx+
(v–v)
β
δ–βv u
dx.
LetV=V+V, where
V=
(u–u)
u–u+
uv)
a(u)+bu+
– uv
au+bu+
dx
= (u–u)
u–u+
uv(au+bu+ ) –uv(au+bu+ )
pp∗
dx
=
–(u–u)+
u–u
pp∗
uv
au+bu+ –uvau+bu+
dx
=
–(u–u)+
pp∗
(auvu–v)(u–u)
+auu+buu+u
(u–u)(v–v)
dx
=
(u–u)
–auvu–v pp∗
+au
u+buu+u
pp∗ (u–u)(v–v)
and
V=
β
(v–v)
δ–βv
u
dx
=
β
(v–v)
δ–βv–v+v
u
=
β
(v–v)
δ–βv–v
u –β
v
u
dx
=
β
(v–v)
δ–βv–v
u –β
v
u
dx
=
(v–v)
δ β –
v–v
u –
v
u
dx
=
–(v–v)
u + (v–v)
δ β –
v
u
dx
=
–(v–v)
u + (v–v)
δu–βv βu
dx
=
–(v–v)
u + (v–v)
δu–δu βu
dx
=
–(v–v)
u +
δ
βu(v–v)(u–u)
dx,
wherep=au+bu+ ,p∗=au
+bu+ ,a= –auvupp∗–v,a=a={ au
u+buu+u pp∗ –
δ βu},
a=u.
Next, we calculateVas follows:
V= –
(u–u,v–v)
a a
a a
(u–u,v–v)T
dx. (.)
It is obvious that dVdt < if and only if the matrix in integrand (.) is positive definite, equivalent to a> andφ(u,v) =aa–aa> , whereφ(u,v) =aa–aa=
( – auvupp∗–v)u – {(au
u+buu+u
pp∗ )
– (auu+buu+u pp∗ )(
δ βu) + (
δ βu)
}> . By condition
(.a)-(.c), we knowa> andφ(u,v) > . Consequently,E∗is globally asymptotically stable.
Thus, we complete this proof.
Next, we give out the conditions of the global asymptotic stability of the boundary equi-libriumE(, ).
Theorem . The boundary equilibrium Eof(.)is globally asymptotically stable if
a+ < βδ+
δ
β (.)
holds.
Proof Define
V(u,v) =
{u– –lnu+v}dx.
Taking the derivative ofVwith regard totalong the trajectory of model (.), we have
˙
where
V=
dv+d
– u
u
dx≤–
d|u|
u dx≤.
Furthermore, we calculateV
and reach
V=
(u– )
–u– uv au+bu+
+v
δ–βv
u
dx
= –
(u– )+
u au+bu+ –
δ βu
(u– )v+βδ u v
dx.
According to condition (.), dVdt < except atE. By LaSalle’s invariance principle,Eis
globally asymptotically stable.
6 Numerical simulations
In this section, to confirm our analytical results found in the previous section, some ex-amples and numerical simulations are presented. We use Matlab (a) to simulate and plot numerical graphs.
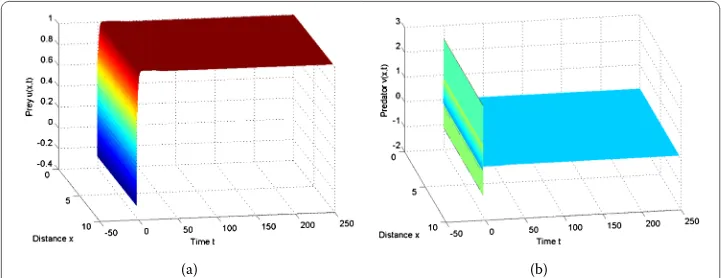
Example If we choosea= .,b= ,δ= .,β= ,d= ,d= , the conditions of
The-orem . are satisfied for system (.). We have that the axial equilibriumE(, ) is globally stable (see Figure ).
Example If we choosea= ,b= ,β= ,d= ,d= ,δ= , the conditions of
Theo-rem . are satisfied for system (.). The positive equilibriumE(., .) is
glob-ally asymptoticglob-ally stable (see Figure ).
Example If we choosea= ,b= .,δ= .,β= .,d= .,d= , then we know
that system (.) has a unique positive homogeneous equilibrium E(., .), which is asymptotically stable (see Figure ). The system undergoes Hopf bifurcation at the equilibriumE∗(see Figure ). By the formulas derived in the previous section, we get c(A)≈.e++ .e+iwith the initial value (., .).
(a) (b)
Figure 1 Numerical simulations of system (1.2) fora= 0.5,β= 1,d1= 1,d2= 100,b= 1,δ= 1.2.The
(a) (b)
Figure 2 Numerical simulations of system (1.2) fora= 1,β= 2,d1= 1,d2= 10,b= 1,δ= 1.The positive
equilibriumE∗of (1.2) is globally asymptotically stable with the initial value (0.8, 0.4).
(a) (b)
Figure 3 Numerical simulations of system (1.2) fora= 7,β= 0.01,d1= 0.1,d2= 10,b= 0.1,δ= 0.2.
The positive equilibriumE∗is locally asymptotically stable with the initial value (0.65, 3.5).
(a) (b)
Figure 4 Numerical simulations of system (1.2) fora= 10,β= 0.01,d1= 0.1,d2= 10,b= 0.1,δ= 0.2.
The positive equilibriumE∗of (1.3) becomes unstable and there exist spatially homogeneous periodic solutions with the initial value (0.65, 3.5).
7 Conclusions
the local stability and global stability of the equilibria, are obtained. Hopf bifurcations are explored by analyzing the characteristic equations. Moreover, the formulas determining the direction and stability of the bifurcating periodic solutions are derived by using the center manifold and the normal form theory of partial functional differential equations. Some numerical simulations are carried out to support our theoretical analysis. In the fu-ture, some challengeable attempts to study the Hopf bifurcation, steady state solution and Turing-Hopf bifurcation of fractional diffusive in a predator-prey system with or without time delay will be proceeded.
Appendix
In this section, we follow the bifurcation formula [] to determine the bifurcation direc-tion of the spatially non-homogeneous periodic soludirec-tions found in Theorem .. When A=AHj,±(j∈N), we calculateRe(C(Aj)). We set
q:=cosj
lx
aj
bj T
=cosj
lx
⎛ ⎝ δ
β(δ+iω+dj l )
⎞ ⎠ T
,
q∗:=cosj
lx
a∗j b∗j
T
=cosj
lx
⎛ ⎝
–iω+δ lπ δ β(iω+δ)(–iω+δ+dj
l ) lπ δ
⎞ ⎠ T
.
From [], we knowq∗,Qqq=q∗,Qq¯q= ¯q∗,Qqq¯= , when j∈N, it follows that we
calculateq∗,Qwq¯,q∗,Qwqandq∗,Cqqq¯. It is straightforward to compute that
iωjI–Lj(Aj) –
= (α+iα)–
iωj+δ+dj
l –B
δ
β iωj+Aj– dj
l
,
iωjI–L(Aj) –
= (α+iα)–
iωj+δ –B δ
β iωj+Aj
,
where
α=
δ+dj
l
Aj–
dj
l
– ωj+Bδ/β,
α= ω
δ+dj
l +Aj–
dj
l
,
α=δAj– ωj +Bδ/β, α= ω
δ+Aj–u∗
.
Then we get
w=
(α+iα)
iωj+δ+dj
l –B
δ
β iωj+Aj– dj
l
cn
dn
cosj
l x
+
(α+iα)
iωj+δ –B δ
β iωj+Aj
cj
dj
,
w=
– α
–δ–djl B
–δβ –Aj+dj l
en
fn
cosj
lx– (α)
–δ B
–δβ –Aj
cj
dj
+lπ
guvτR
β(δμ+ω)
δ
δμ β(μ+ω)–
βω(δ–μ) δ
δω β(μ+ω)
–guvτI
β(δμ+ω) δ
δω β(μ+ω)+
βω(δ–μ) δ
δμ β(μ+ω)
+
fuuu+
δ(μ+ω) β(μ+ω)fuuv+
β(δμ+ω)
δ guuu
+
δμ+ μω+δω δ(μ+ω) guuv
+
δ[(δμ+ω)( +μ–ω) + μω(δ–μ)]
β(μ+ω) guvv
.
Thus the bifurcating periodic solution is supercritical (resp. subcritical) if
α(AHj )Re(C(A H
j )) < (resp. > ).
Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 11601543), the Natural Science and Technology Foundation of Henan Province (No.15A110046), the Education Department Foundation of Henan Province (No. 15A110046 and 13A110101) and the Research Innovation Project of ZhouKou Normal University (no. ZKNUA201303).
Declarations
The author declares that there is no conflict of interests regarding the publication of this paper.
Competing interests
The author declares that she has no competing interests.
Authors’ contributions
The author contributed equally to the writing of this paper. The author read and approved the final manuscript.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Received: 14 March 2017 Accepted: 10 August 2017
References
1. Kalmár-Nagy, T, Stépán, G, Moon, FC: Subcritical Hopf bifurcation in the delay equation model for machine tool vibrations. Nonlinear Dyn.26(2), 121-142 (2001)
2. Rietkerk, M, Dekker, SC, de Ruiter, PC, van de Koppel, J: Self-organized patchiness and catastrophic shifts in ecosystems. Science305(5692), 1926-1929 (2004)
3. Field, RJ, Noyes, RM: Oscillations in chemical systems. IV. Limit cycle behavior in a model of a real chemical reaction. J. Chem. Phys.60(5), 1877-1884 (1974)
4. Angeli, D, Ferrell, JE, Sontag, ED: Detection of multistability, bifurcations, and hysteresis in a large class of biological positive-feedback systems. Proc. Natl. Acad. Sci. USA101(7), 1822-1827 (2004)
5. Xiao, M, Cao, J: Hopf bifurcation and non-hyperbolic equilibrium in a ratio-dependent predator-prey model with linear harvesting rate. Math. Comput. Model.50(3), 360-379 (2009)
6. Huang, C, Cao, J, Xiao, M, Alsaedi, A, Alsaadi, FE: Controlling bifurcation in a delayed fractional predator-prey system with incommensurate orders. Appl. Math. Comput.293, 293-310 (2017)
7. Xu, W, Hayat, T, Cao, J, Xiao, M: Hopf bifurcation control for a fluid flow model of Internet congestion control systems via state feedback. IMA J. Math. Control Inf.33(1), 69-93 (2016)
8. Xu, W, Cao, J, Xiao, M: Bifurcation analysis of a class of (n+ 1)-dimension Internet congestion control systems. Int. J. Bifurc. Chaos Appl. Sci. Eng.25(2), 1550019 (2015)
9. Cheng, Z, Wang, Y, Cao, J: Stability and Hopf bifurcation of a neural network model with distributed delays and strong kernel. Nonlinear Dyn.86(1), 323-335 (2016)
10. Xu, W, Cao, J, Xiao, M, Ho, DWC, Wen, G: A new framework for analysis on stability and bifurcation in a class of neural networks with discrete and distributed delays. IEEE Trans. Cybern.45(10), 2224-2236 (2015)
11. Huang, C, Meng, Y, Cao, J, Alsaedi, A, Alsaadi, FE: New bifurcation results for fractional BAM neural network with leakage delay. Chaos Solitons Fractals100, 31-44 (2017)
12. Huang, C, Cao, J, Xiao, M: Hybrid control on bifurcation for a delayed fractional gene regulatory network. Chaos Solitons Fractals87, 19-29 (2016)
13. Huang, C, Cao, J, Xiao, M, Alsaedi, A, Hayat, T: Bifurcations in a delayed fractional complex-valued neural network. Appl. Comput. Math.292, 210-227 (2017)
15. Yang, Y, Xu, Y: Global stability of a diffusive and delayed virus dynamics model with Beddington-DeAngelis incidence function and CTL immune response. Comput. Math. Appl.71(4), 922-930 (2016)
16. Yi, F, Wei, J, Shi, J: Global asymptotical behavior of the Lengyel-Epstein reaction-diffusion system. Appl. Math. Lett. 22(1), 52-55 (2009)
17. Peng, R, Shi, J: Non-existence of non-constant positive steady states of two Holling type-II predator-prey systems: strong interaction case. J. Differ. Equ.247(3), 866-886 (2009)
18. Ko, W, Ryu, K: Non-constant positive steady-states of a diffusive predator-prey system in homogeneous environment. Aust. J. Math. Anal. Appl.327(1), 539-549 (2007)
19. Zeng, X, Liu, Z: Nonconstant positive steady states for a ratio-dependent predator-prey system with cross-diffusion. Nonlinear Anal., Real World Appl.11(1), 372-390 (2010)
20. Li, S, Wu, J, Nie, H: Steady-state bifurcation and Hopf bifurcation for a diffusive Leslie-Gower predator-prey model. Comput. Math. Appl.70(12), 3043-3056 (2015)
21. Cholewa, JW, Dlotko, T: Global Attractors in Abstract Parabolic Problems. Cambridge University Press, Cambridge (2000)
22. Ye, Q, Li, Z, Wang, M, Wu, Y: Introduction to Reaction-Diffusion Equations. Chinese Science Press, Beijing (1990) 23. Wu, J: Theory and Applications of Partial Functional Differential Equations. Springer, New York (2012) 24. Hassard, BD, Kazarinoff, ND, Wan, YH: Theory and Applications of Hopf Bifurcation. Cambridge University Press,
Cambridge (1981)