Cryptography and Network Security Chapter 2

Cryptography and Network Security

Chapter 2

Fifth Edition

by William Stallings

Contents

●

Symmetric Cipher Model

Substitution Techniques

Transposition Techniques

Rotor Machines

Ciphers

●

Symmetric cipher:

same key used for encryption

and decryption

–

Block cipher:

encrypts a block of plaintext at a time

(typically 64 or 128 bits)

–

Stream cipher:

encrypts data one bit or one byte at a

time

●

Asymmetric cipher:

different keys used for

encryption and decryption

Symmetric Encryption

●

or conventional / private-key / single-key

sender and recipient share a common key

●

all classical encryption algorithms are private-key

was only type prior to invention of public-key in

1970’s

Some Basic Terminology

●

plaintext - original message ●

ciphertext - coded message

●

cipher - algorithm for transforming plaintext to ciphertext ●

key - info used in cipher known only to sender/receiver ●

encipher (encrypt) - converting plaintext to ciphertext

●

decipher (decrypt) - recovering plaintext from ciphertext ●

cryptography - study of encryption principles/methods

●

cryptanalysis (codebreaking) - study of principles/ methods of deciphering ciphertext without knowing key

●

Requirements and Assumptions

●

Requirements for secure use of symmetric

encryption:

1. Strong encryption algorithm: Given the algorithm and ciphertext, an attacker cannot obtain key or plaintext 2. Sender/receiver know secret key (and keep it secret)

●

Assumptions:

1. Cipher is known

Model of Symmetric Cryptosystem

Intended receiver can calculate: X = D(K;Y )

Attacker knows E, D and Y . Aim: Determine plaintext:

Characterising Cryptographic Systems

● Operations used for encryption:

– Substitution replace one element in plaintext with another – Transposition re-arrange elements

– Product systems multiple stages of substitutions and transpositions

● Number of keys used:

– Symmetric sender/receiver use same key (single-key,secret-key, shared-key, conventional)

– Public-key sender/receiver use different keys (asymmetric)

● Processing of plaintext:

Cryptanalysis

●

Objective of attacker: recover key (not just

message)

●

Approaches of attacker:

– Cryptanalysis Exploit characteristics of algorithm to deduce plaintext or key

– Brute-force attack Try every possible key on ciphertext until intelligible translation into plaintext obtained

●

If either attack finds key, all future/past messages

Cryptanalytic Attacks

●

ciphertext only

– only know algorithm & ciphertext, is statistical,

know or can identify plaintext

●

known plaintext

– know/suspect plaintext & ciphertext

●

chosen plaintext

– select plaintext and obtain ciphertext

●

chosen ciphertext

– select ciphertext and obtain plaintext

●

chosen text

Measures of Security

●

Unconditionally Secure

– Ciphertext does not contained enough information to derive plaintext or key

– One-time pad is only unconditionally secure cipher (but not very practical)

●

Computationally Secure

– If either:

» Cost of breaking cipher exceeds value of encrypted information » Time required to break cipher exceeds useful lifetime of encrypted

information

– Hard to estimate value/lifetime of some information

Brute Force Search

●

always possible to simply try every key

most basic attack, proportional to key size

assume either know / recognise plaintext

Key Size (bits) Number of Alternative Keys

Time required at 1 decryption/µs

Time required at 106 decryptions/µs

32 232 = 4.3 × 109 231 µs = 35.8 minutes 2.15 milliseconds

56 256 = 7.2 × 1016 255 µs = 1142 years 10.01 hours

128 2128 = 3.4 × 1038 2127 µs = 5.4 × 1024 years 5.4 × 1018 years

168 2168 = 3.7 × 1050 2167 µs = 5.9 × 1036 years 5.9 × 1030 years

26 characters (permutation)

26! = 4 × 1026 2 × 1026 µs = 6.4 × 1012 years 6.4 × 106 years

Substitution Ciphers - Caesar Cipher

●

earliest known substitution cipher

●

replaces each letter by 3rd letter on

●

:example

meet me after the toga party

PHHW PH DIWHU WKH WRJD SDUWB

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Caesar Cipher

● Generalised Caesar Cipher

– Allow shift by k positions

– Assume each letter assigned number (a = 0, b = 1, . . . )

– then have Caesar cipher as:

c = E(k, p) = (p + k) mod (26)

(plain letter index + key) mod (total number of letters)

p = D(k, c) = (c – k) mod (26)

(ciper letter index - key) mod (total number of letters)

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Security of Caesar Cipher

● Key space: {0, 1, ..., 25}

● Brute force attack

– Try all 26 keys, e.g. k = 1, k = 2, . . . – Plaintext should be recognised

● How to improve against brute force?

– Hide the encryption/decryption algorithm: Not practical

– Compress, use different language: Limited options

Monoalphabetic Cipher

● use a single alphabet for both plaintext and ciphertext

● Arbitrary substitution: one element maps to any other element

● n element alphabet allows n! permutations or keys

● :Example

– Plain : a b c d e ... w x y z

– Cipher: D Z G L S ... B T F Q

● . . . Try brute force

– Caesar cipher: 26 keys

– Monoalphabetic (English alphabet): 26! = 4 x 1026 keys

Monoalphabetic Cipher example

3.18 We can use the key in the below Figure to encrypt the message

Examples of Monoalphabetic Ciphers

The following shows a plaintext and its corresponding ciphertext. The cipher is probably monoalphabetic

because both l’s are encrypted as O’s. Example

The following shows a plaintext and its corresponding ciphertext. The cipher is not monoalphabetic

Monoalphabetic Cipher Security

●

now have a total of 26! = 4 x 10

keys

●

With so many keys, it is secure against brute-force

attacks.

Attacks on Monoalphabetic Ciphers

● Exploit the regularities of the language

– Frequency of letters, digrams, trigrams

– Expected words

● Fundamental problem with monoalphabetic ciphers

– Ciphertext reflects the frequency data of original

English Letter Frequencies

eg "th lrd s m shphrd shll nt wnt"

letters are not equally commonly used

in English E is by far the most common letter

followed by T,R,N,I,O,A,S

Example Cryptanalysis

●

given ciphertext:

UZQSOVUOHXMOPVGPOZPEVSGZWSZOPFPESXUDBMETSXAIZ VUEPHZHMDZSHZOWSFPAPPDTSVPQUZWYMXUZUHSX

EPYEPOPDZSZUFPOMBZWPFUPZHMDJUDTMOHMQ

●

count relative letter frequencies (see text)

guess P & Z are e and t

●

guess ZW is th and hence ZWP is the

●

proceeding with trial and error finally get:

it was disclosed yesterday that several informal but

Polyalphabetic Ciphers

●

polyalphabetic substitution ciphers

– A sequence of monoalphabetic ciphers (M₁, M₂, M₃, ..., M_k) is used in turn to encrypt letters.

– A key determines which sequence of ciphers to use.

– Each plaintext letter has multiple corresponding ciphertext letters. – This makes cryptanalysis harder since the letter frequency

distribution will be flatter

.

●

Examples:

– Vigenere cipher

Vigenère Cipher

●

Simplest polyalphabetic substitution cipher

Consider the set of all Caesar ciphers:

{ C

, C

, C

, ..., C

}

●

Key: e.g. security

●

Encrypt each letter using

in turn.

●

Repeat from start after C

y

.

●

Decryption simply works in reverse.

Vigenere cipher example

3.26 Note that the Vigenere key stream does not depend

on the plaintext characters;

Vigenere cipher example

3.27 Encrypt the message “She is listening” , using the 6-character

Security of Vigenère Ciphers

Is it Breakable?

● Yes , Vigenere ciphers, like all polyalphabetic ciphers, do not preserve the

frequency of the characters.

The cryptanalysis of Vigenère Ciphers

● The cryptanalysis here consists of two parts :

– finding the length of the key and finding the key itself.

– Kaiski test

» the cryptanalyst searches for repeated text segments, of at least three

characters,

» finds their distance, d₁, d₂, …, d_n, in the ciphertext. » Then gcd(d₁, d₂, …, d_n)/m where m is the key length.

–

cryptanalysis of Vigenère Ciphers example

3.30 Let us assume we have intercepted the following ciphertext:

Example

cryptanalysis of Vigenère Ciphers example

(cont.)

3.31 The greatest common divisor of differences is 4, which means that the key length is multiple of 4. First try m = 4.

An unconditionally Secure Cipher

One-Time Pad

●

if a truly random key as long as the message is

used, the cipher will be secure

●

called a One-Time pad

●

is unbreakable since ciphertext bears no statistical

relationship to the plaintext

●

since for

any plaintext

&

any ciphertext

there

exists a key mapping one to other

●

can only use the key

once

though

●

Transposition Ciphers

●

now consider classical

transposition

or

permutation

ciphers

●

these hide the message by rearranging the letter

order

●

without altering the actual letters used

●

can recognise these since have the same frequency

Keyless Transposition Ciphers –Rail fence

Ciphers

3.35

•A good example of a keyless cipher using the first method ,is the rail fence cipher.

•write message letters out diagonally over a number of rows

•then read off cipher row by row

3.36 Alice and Bob can agree on the number of columns.

Alice writes the same plaintext, row by row, in a table of four columns.

Example 3.23

She then creates the ciphertext “MMTAEEHREAEKTTP”.

Keyless Transposition Ciphers – Row

Keyed Transposition Ciphers - Row

Transposition Ciphers

● Is a more complex transposition

● write letters of message out in rows over a specified number of columns

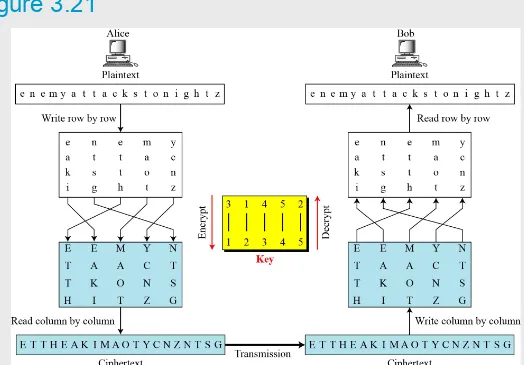
● then reorder the columns according to some key before reading off the rows

– Plaintext is written row by row in a rectangle.

– Ciphertext: write out the columns in an order specified by a key.

Example:

Key: 3 4 2 1 5 6 7

Ciphertext:

TTNAAPTMTSUOAODWCOIXKNLYPETZ

a t

t

a

c k p

o s

t

p

o n e

d u

n

t

i l t

Row Transposition Ciphers – encryption /de

3.38

Double Transposition

●

Product Ciphers

●

ciphers using substitutions or transpositions are

not secure because of language characteristics

●

hence consider using several ciphers in succession

to make harder, but:

– two substitutions make a more complex substitution – two transpositions make more complex transposition – but a substitution followed by a transposition makes a

new much harder cipher

Rotor Machines

●

Multiple stages of encryption can be used for substitution and transposition ciphers

●

Rotor machines were early application of this

●

Machine has multiple cylinders

●

Monoalphabetic substitution cipher for each cylinder

●

Output of one cylinder is input to next cylinder

●

Plaintext is input to first cylinder; ciphertext is output of last cylinder

●

Entering a plaintext letter causes last cylinder to rotate its cipher

●

Complete rotation of one cylinder causes previous cylinder to rotate its cipher

●

Steganography

● an alternative to encryption

● hides existence of message

– using only a subset of letters/words in a longer message marked in some way

– using invisible ink

– hiding in LSB in graphic image or sound file ● has drawbacks

– Once attacker knows your method, everything is lost – Can be inecient (need to send lot of information to – carry small message)

Summary

●

:have considered

–

classical cipher techniques and terminology

–

monoalphabetic substitution ciphers

–

cryptanalysis using letter frequencies

–

polyalphabetic ciphers

–

transposition ciphers

–

product ciphers and rotor machines