Resource Allocation in Project Scheduling Application of Fuzzy AHP

Resource Allocation in Project Scheduling Application of Fuzzy AHP

Several approaches are followed in project scheduling under multiple resources. Typically, priorities for each activity are obtained using qualitative data. In this paper, both quantitative and qualitative data are considered in a fuzzy environment. A Fuzzy Analytical Hierarchy process is developed to obtain weightages for each activity that needs multiple resources. Fuzzy AHP efficiently handles the fuzziness of data. A hierarchical structure is constructed for the resources consumed in the project network. A weighted sum of resources for each activity is obtained and the activities are ranked based on weighted sum and scheduled. The method is explained through numerical illustration.

1.

Introduction

The project schedule is a tool that communicates what work needs to be performed, which resources of the organization will perform the work and the timeframes in which that work needs to be performed. The project schedule should reflect all of the work associated with delivering the project on time. Without a full and complete schedule, the project manager will be unable to communicate the complete effort, in terms of cost and resources, necessary to deliver the project.

Resource allocation is used to assign the available resources in an economic way. It is part of resource management. In project management, resource allocation is the scheduling of activities and the resources required by those activities while taking into consideration both the resource availability and the project time [21]. The (RCPSP) consists in scheduling a set of activities linked by precedence relations in order to minimize project duration, while satisfying precedence and resource constraints [25].

Several approaches have been followed for project scheduling with resource allocation. An integer programming problem is a mathematical optimization or feasibility program in which some or all of the variables are restricted to be integers. RCPSP is NP-hard optimization problem [4]. A special case is 0-1 integer linear programming, in which the unknowns are binary. Mixed integer programming has many applications in industrial production, including job-shop modelling. A possible objective is to maximize the total production, without exceeding the available resources. In some cases, this can be expressed in terms of a linear program, but variables must be constrained to be integer.

Dynamic programming is an optimization approach that transforms a complex problem into a sequence of simpler problems; it’s essential characteristic is the multistage nature of the optimization procedure. More so than the optimization techniques described previously, dynamic programming provides a general frame work for analyzing many problem types. Robinson [26] provides a conceptual dynamic programming framework for solving the problem in general project networks, but does not provide any algorithm. Hindelang and Muth [15] were the first to provide a complete dynamic programming formulation for use in decision CPM networks. Demeulemeester et al. [8] presented two algorithms called as exact network reduction procedures for activity-on-the-arc networks based on dynamic programming logic, which exploit network reduction. Rothfarb et al. [27] and Frank et al. [11] developed a serial and parallel merge algorithm for the optimization of the succession of series and parallel optimization of the series/parallel reducible projects. Elmaghraby [9] has shown that the optimal allocation of resources in project that is composed solely of a set of activities in series or in parallel can be secured through the application of dynamic programming. The serial optimization can be viewed as a series arc reduction.

The completion time under no resource constraints is less than when constraints are imposed. Optimal solutions to this problem are very difficult to obtain, especially for large-scale networks by the application of the programming approaches. One way of approaching this problem is to use heuristic techniques. A heuristic is a set of decision rules that might lead to an optimum solution but does not guarantee optimality. In other words, the heuristic solution may result in an optimum solution for some problems and may not for other problems.

Several heuristic methods have been proposed to treat this problem in different contexts. Elsayed [10] developed a heuristic algorithm for assigning resources to activities such that project duration is minimized. The criterion for allocating a single type of resource to the activities in the network is based on ROT (resource over time), which is calculated as the maximum ROT value that an activity controls through the network on any one path.

Brook’s [5] developed a heuristic algorithm ACTIM (activity time) similar to those under ROT except that the ranking of the activities in the table is dependent on the ACTIM value of an activity. The ACTIM value of an activity is calculated as the maximum time that the activity controls through the network on any one path.

Bedworth [3] developed a heuristic algorithm ACTRES (activity resources) similar to those of ACTIM with the exception that the ranking of the activities is based on their ACTRES values. The ACTRES value of an activity is calculated by multiplying each activity’s time by its resource and then finding the maximum ACTRES that an activity controls through the network on any path.

and ACTRES. The value of TIMRES of an activity is calculated as the sum of ACTIM and ACTRES values of this activity. Whitehouse and Brown [33] developed a heuristic algorithm GENRES by modifying the TIMRES criterion to obtain the least possible project completion time. The project scheduling can be generated using combination of ACTIM and ACTRES which are not equally weighted

Nasr [22] mentioned a criteria TMROS which is an improvement in the criteria: ACROS and ACTIM. The ACROS criterion of an activity is calculated as the maximum resource value it controls through the network on any path. The method of calculating ACROS for each activity is similar to that used in calculating ACTIM, but resource values are used instead of time values.

Neumann and Zhan [23] proposed an efficient priority-rule heuristics for solving the resource-constrained project-scheduling problem. Hartmann [12] proposed the branch and bound method for solving the (RCPSP). Shue and Zamani [29] proposed the Admissible heuristic Search algorithm for solving the (RCPSP). Lee et al. [19] proposed a novel market mechanism called precedence cost tatonnement (P-TATO), which solves individual resource-constrained local resource scheduling in an optimal way and searches for a precedence conflict-free scheduling through a tatonnement type procedure. Herroelen [14] proposed a generic hierarchical project planning and control framework that serves to position the various project planning procedures and discuss important research opportunities, the exploration of which may help to close the theory-practice gap. Kolisch and Hartmann [17] proposed the forward-backward improvement technique for the (RCPSP). Banaszak and Zaremba [2] proposed a heuristic method for process planning and scheduling. The method is based on critical path approach and the branch and bound search scheme. Hasgul et al. [13] proposed an agent-based architecture for (RCPSP). Oddi et al. [24] proposed an iterative flattering search (IFS) a met-heuristic for solving (RCPSP).

Analytical hierarchy process (AHP) method developed by Satty [28] has been widely used for selecting the best alternative. So the application of Satty’s AHP has some shortcomings as follows (1) the AHP method is mainly used in nearly crisp decision applications, (2) The AHP method creates and deals with a very unbalanced scale of judgment, (3) The AHP method does not take into account the uncertainty associated with the mapping of one’s judgment to a number, (4) Ranking of the AHP method is rather imprecise, (5) The subjective judgment, selection and preference of decision makers have great influence on the AHP results. It is also renowned that human assessment on qualitative attributes is always subjective and thus imprecise. Therefore conventional AHP seems not enough to confine decision maker’s requirements clearly. In order to model this sort of uncertainty in human preference, fuzzy sets could be included with the pairwise comparison as an extension of AHP. The fuzzy AHP approach allows a more precise description of the decision making process.

In this paper a fuzzy AHP approach is proposed to make up the ambiguity and uncertainty offered in the magnitude attributed to judgment of the decision maker, because the pair wise comparison in the conventional AHP seems to insufficient and imprecise to confine the degree of importance of decision maker. So, fuzzy logic is introduced in the pair wise comparison of AHP.

2.

Fuzzy Analytical Hierarchy Process

The fuzzy AHP is the fuzzy addition of AHP to proficiently handle the fuzziness of the data drawn in the decision making. It is easier to understand and it can be effectively handle both qualitative and quantitative data in the multi-attribute decision making problems. In this approach triangular fuzzy numbers are used for the preferences of one criterion over another and then the pair wise comparison is calculated [31].

To contract with vagueness of human thought, Zadeh [18] first proposed the fuzzy set theory, which was oriented to the rationality of uncertainty due to ambiguity or vagueness. A major contribution of fuzzy set theory is its ability of representing vague data. The theory also allows mathematical operators and programming to pertain to the fuzzy domain. A fuzzy set is a class of objects with a range of grades of membership. Such a set is characterized by a membership (characteristic) function, which assigns to each object a grade of membership ranging between zero and one. A tilde “~” will be positioned above a symbol if the symbol represents a fuzzy set.

Though the purpose of AHP is to capture the expert’s knowledge, the conventional AHP still cannot reflect the human thinking style. Therefore, fuzzy AHP, a fuzzy extension of AHP, was developed to solve the hierarchical fuzzy problems. In the fuzzy-AHP procedure, the pairwise comparisons in the judgment matrix are fuzzy numbers that are modified by the designer’s emphasis [7].

3.

Fuzzy Representation of Pairwise Comparison

The hierarchy of the resources needs to be established before performing the pairwise comparison of AHP. In conventional AHP, the pairwise is made by using a ratio scale. A frequently used scale is the nine-point scale 1-9 (Table 1) which shows the judgments or preferences among the options such as equally important, weakly more important, strongly more important, very strongly more important and extremely more important preferred.

In this study triangular fuzzy numbers1-9, are used to represent subjective pairwise comparisons of selection process in order to capture the vagueness. A fuzzy number is a special fuzzy set F= , ( ) , where x takes the values on the real line, R:-∞ < x < +∞ and µ ( ) is a continuous mapping from R to the closed interval [0, 1]. A triangular fuzzy number denoted as = (l, m, u), where l ≤ m≤ u, has the following triangular type membership function;

0 x < l x - l m - l l≤ x ≤ m

µF(x) = u - x u – m m≤ x ≤ u

0 x > u

Alternatively, by defining the interval of confidence level α, triangular fuzzy number can be characterized as

∀ [0, 1] = [lα , µα] = [(m-l)α +l, -(u-m)α +u]

Some major operations for positive fuzzy numbers are described by the interval of confidence, by Kaufmann and Gupta [16] as given below ∀ , , , R+, α = [ , ], α = [ , ], α ϵ [0,1] ⊕ = [ + , + ] Θ = [ − , − ] ⨂ = [ , ] / = [ ⁄ , ∕ ]

Table 1Definition and Membership Function of Fuzzy Number Ayag [1]

Intensity of importance Fuzzy number Definition Membership function

1 1 Equally important/preferred (1,1,2)

3 3 Moderately more important/preferred (2,3,4)

5 5 Strongly more important/preferred (4,5,6)

7 7 Very strongly more important/preferred (6,7,8)

9 9 Extremely more important/preferred (8,9,10)

a

Fundamental scale used in pair wise comparison Satty [32]

Figure 1 Fuzzy Membership Function for Linguistic Values for Attributes or Alternatives

The triangular fuzzy numbers, 1-9, are utilized to steps forward the conventional nine-point scale scheme. In order to take the vagueness of human qualitative assessment into consideration, the five triangular fuzzy numbers are defined with the corresponding membership function as shown in Fig.1.

The steps of fuzzy AHP Approach

The AHP method is also known as an eigenvector method. It indicates that the eigenvector consequent to the largest eigenvalue of the pairwise comparisons matrix provides the relative priorities of the factors, and preserves ordinal preferences among the alternatives. This means that if an substitute is preferred to another. A vector of weights obtained from the pairwise comparisons matrix reflects the relative performance of the various factors. Cheng and Mon [6] explained that in the fuzzy AHP triangular fuzzy numbers are utilized to progress the scaling scheme in the judgment matrices, and interval arithmetic is used to solve the fuzzy eigenvector.

The four-step-procedure of this approach is given as

Step1. Comparing the performance score: triangular fuzzy numbers (1, 3, 5, 7, 9 ) are used to indicate the relative strength of each pair of elements in the same hierarchy.

Step2. Constructing the fuzzy comparison matrix: By using triangular fuzzy numbers, via pairwise comparison, the fuzzy judgment matrix is constructed as given below;

1 … … 1 … … = … … … … … … … … … … 1

Where, = 1, if I is equal j, and = 1, 3, 5, 7, 9 or 1-1 , 3-1

, 5-1 , 7-1

, 9-1

, if i is not equal j. Step 3. Solving fuzzy eigenvalue: A fuzzy eigenvalue, is a fuzzy number solution to = (1)

Where is n×n fuzzy matrix containing fuzzy numbers and is a non-zero nx1, fuzzy vector containing fuzzy number . To perform fuzzy multiplications and additions by using the interval arithmetic and α – cut, the equation = is equivalent to [ , ]⊕ ⋯ ⊕[ , ] = [ , ] Where, = , = ( , … … , ) α = , , α = [ , ], α = [ , ] (2)

for 0 < α ≤ 1 and all i, j, where i= 1,2,….,n, j = 1, 2, …., n

α – cut is known to incorporate the experts or decision maker(s) confidence over his/her preference or the judgments. Degree of satisfaction for the judgment matrix is estimated by the index of optimism µ. The larger value of index µ indicates the

higher degree of optimism. The index of optimism is a linear convex combination (Lee, 1999) defined as

= + (1− ) , ∀ ∈ [0, 1] (3) While the α is fixed, the following matrix can be obtained after setting the index of optimism, µ, in order to estimate the

degree of satisfaction.

Figure 2 α –Cut Operation on Triangular Fuzzy Number

1 ⋯ ⋯ 1 ⋯ ⋯ = ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ 1

The eigen vector is calculated by fixing the µ value and identifying the maximal eigenvalue. α – cut: It will yield an interval set of values from a fuzzy number. For example, α = 0.5 will yield a set α0.5 = (2,3,4). The operation is presented by using Table 1 (Fig.2).

Normalization of both the matrix of paired comparisons and calculation of priority weights (approx. attribute weights), and the matrices and priority weights for alternatives are also done before calculating λmax. in order to control the result of the method, the consistency ratio for each of the matrices and overall inconsistency are expressed by the following equation CI, and the measure of inconsistency is called the CI,

= (4) The consistency ratio (CR) is used to estimate directly the consistency of pairwise comparisons. The CR is computed by

dividing the CI by a value obtained from a table of Random Consistency Index (RI);

= (5) If the CR less than 0.10, the comparisons are acceptable, otherwise not. RI is the average index for randomly generated weights (Satty, 1981).

Step 4. The priority weight of each alternative can be obtained by multiplying the matrix of evaluation ratings by the vector of attribute weights and summing over all attributes. Expresses in conventional mathematical notation;

Weighted evaluation for alternative

=∑ ( ℎ × ) (6)

For i= 1,2,…., t ( t: total number of attributes)

After calculating the weight of each alternative, the overall consistency index is calculated to make sure that it is smaller than 0.10 for consistency on judgments.

4.

Illustrative Example

Table2 Activity Duration

(days) Predecessors

Resource Requirements per day R1 R2 R3 R4 R5 R6 A 6 - 5 2 2 2 7 4 B 3 - 3 5 2 3 9 6 C 4 A 2 4 4 2 3 1 D 6 - 5 4 3 5 5 4 E 7 A,B 3 5 2 3 8 0 F 5 C 4 1 4 9 2 5 G 2 D 4 1 4 3 9 8 H 2 A,B 5 5 4 0 9 1 I 2 G,H 3 2 4 3 4 2 J 6 F 1 5 4 6 7 3 K 1 C,E 3 3 2 4 5 1 L 2 E,G,H 3 2 2 8 3 4 M 4 I,K 2 2 2 2 4 8 N 2 F,L 1 4 4 3 4 1 O 3 L 5 5 4 6 2 3 P 5 J,M,N 3 2 3 4 7 8 Q 8 O 4 5 4 2 3 4 R 2 D,O 5 3 3 3 7 8 S 6 P,R 2 4 6 2 3 4 T 2 Q 1 6 2 7 5 2

Daily Resource Limit 7 10 10 16 18 13

Here Table 2 shows the example taken for illustration [31]. Table 2 gives the information about the activities, their duration, precedence relationship of each activity and the resources required for each activity.

The lower limit and the upper limit of the fuzzy numbers with respect to α are distinct as follows by applying Eq. 2:

1α = [1, 3-2α],

3α = [1+2α, 5- 2α], 3α-1 = , , 5α = [3+2α, 7- 2α], 5α-1 = , , 7α = [5+2α, 9- 2α], 7α-1 = , , 9α = [7+2α, 11- 2α], 9α-1 = , .

Figure 3Hierarchical Tree of the AHP

Solution Procedure

Step1: Developing the Fuzzy comparison matrix of the attributes using triangular fuzzy numbers. Step2: Developing the α-cuts fuzzy comparison matrix for the attributes (α = 0.5, µ = 0.5)

Step3: Developing the normalized comparison matrix for the fuzzy comparison matrix by dividing the each element in the column by the sum of that particular column.

Step4: Establishing priority vector Step5: Comparison of alternatives

Step6: Calculating priority vector for alternatives Step7: Obtain the overall priority vector

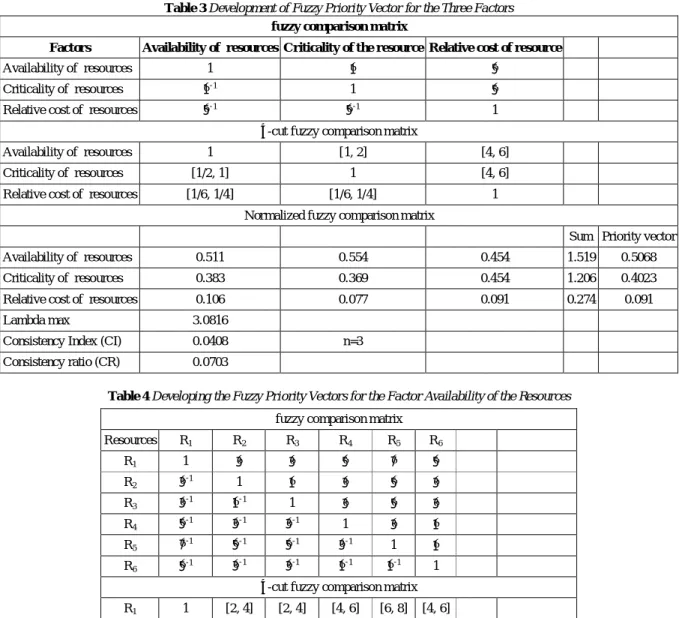
Table 3Development of Fuzzy Priority Vector for the Three Factors

fuzzy comparison matrix

Factors Availability of resources Criticality of the resource Relative cost of resource

Availability of resources 1 1 5

Criticality of resources 1-1 ₁

5

Relative cost of resources 5-1 ₅-1 ₁

α-cut fuzzy comparison matrix

Availability of resources 1 [1, 2] [4, 6]

Criticality of resources [1/2, 1] 1 [4, 6]

Relative cost of resources [1/6, 1/4] [1/6, 1/4] 1

Normalized fuzzy comparison matrix

Sum Priority vector

Availability of resources 0.511 0.554 0.454 1.519 0.5068

Criticality of resources 0.383 0.369 0.454 1.206 0.4023

Relative cost of resources 0.106 0.077 0.091 0.274 0.091

Lambda max 3.0816

Consistency Index (CI) 0.0408 n=3

Consistency ratio (CR) 0.0703

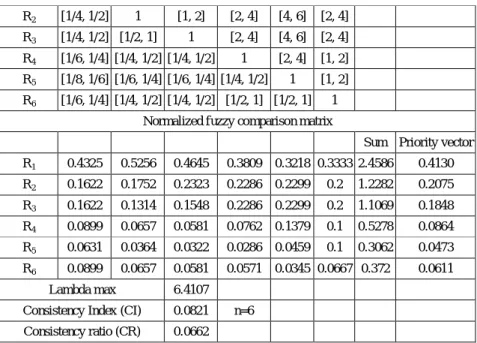
Table 4Developing the Fuzzy Priority Vectors for the Factor Availability of the Resources

fuzzy comparison matrix

Resources R1 R2 R3 R4 R5 R6 R1 1 3 3 5 7 5 R2 3-1 1 1 3 5 3 R3 3-1 1-1 1 3 5 3 R4 5-1 3-1 3-1 1 3 1 R5 7-1 5-1 5-1 3-1 1 1 R6 5-1 3-1 3-1 1-1 1-1 1

α-cut fuzzy comparison matrix R1 1 [2, 4] [2, 4] [4, 6] [6, 8] [4, 6]

R2 [1/4, 1/2] 1 [1, 2] [2, 4] [4, 6] [2, 4]

R3 [1/4, 1/2] [1/2, 1] 1 [2, 4] [4, 6] [2, 4]

R4 [1/6, 1/4] [1/4, 1/2] [1/4, 1/2] 1 [2, 4] [1, 2]

R5 [1/8, 1/6] [1/6, 1/4] [1/6, 1/4] [1/4, 1/2] 1 [1, 2]

R6 [1/6, 1/4] [1/4, 1/2] [1/4, 1/2] [1/2, 1] [1/2, 1] 1

Normalized fuzzy comparison matrix

Sum Priority vector R1 0.4325 0.5256 0.4645 0.3809 0.3218 0.3333 2.4586 0.4130 R2 0.1622 0.1752 0.2323 0.2286 0.2299 0.2 1.2282 0.2075 R3 0.1622 0.1314 0.1548 0.2286 0.2299 0.2 1.1069 0.1848 R4 0.0899 0.0657 0.0581 0.0762 0.1379 0.1 0.5278 0.0864 R5 0.0631 0.0364 0.0322 0.0286 0.0459 0.1 0.3062 0.0473 R6 0.0899 0.0657 0.0581 0.0571 0.0345 0.0667 0.372 0.0611 Lambda max 6.4107 Consistency Index (CI) 0.0821 n=6 Consistency ratio (CR) 0.0662

The corresponding fuzzy priority vectors for the factors criticality of the resources and the relative cost of the resources calculations are carried out in the same manner as availability of the resources and the final priority vectors are shown in Table 5.

As the value of CR is less than 0.1, the judgments are acceptable.

Table 5Ranking of Activities- Overall Priority

Availability of resources Criticality of the resources Relative cost of the resources

Resources 0.5068 0.4023 0.091 Overall priority

R1 0.4130 0.4173 0.4174 0.4151 R2 0.2075 0.2096 0.2097 0.2085 R3 0.1848 0.1715 0.1715 0.1781 R4 0.0864 0.0873 0.0873 0.0868 R5 0.0473 0.0644 0.0592 0.0552 R6 0.0611 0.0498 0.0550 0.0559 Sum 0.9996

From table 5, the overall priority vector for the resources is obtained. This overall priority vector for the resources will become the weightages of the resources.

Estimating the weighted sum for each activity using the weightages of the resources for each activity using the formula and ranking the activities according to the weighted sum of the activities.

=∑ ( )

Where ij is the value of the resource required for the activity j; maxj and minj are the maximum and minimum values of criterion j among all activities.

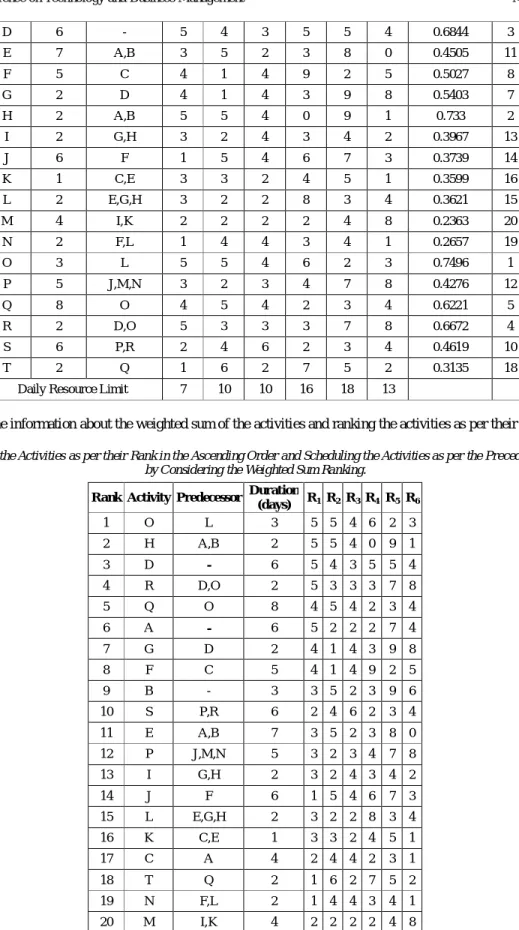
Table 6 Weighted Sum of the Activities

Activity Duration

(days) Predecessors

Resource Requirements per day

Weighted sum Ws Rank R1 R2 R3 R4 R5 R6 W1 W2 W3 W4 W5 W6 0.4151 0.2085 0.1781 0.0868 0.0552 0.0559 A 6 - 5 2 2 2 7 4 0.5434 6 B 3 - 3 5 2 3 9 6 0.5003 9 C 4 A 2 4 4 2 3 1 0.3518 17

D 6 - 5 4 3 5 5 4 0.6844 3 E 7 A,B 3 5 2 3 8 0 0.4505 11 F 5 C 4 1 4 9 2 5 0.5027 8 G 2 D 4 1 4 3 9 8 0.5403 7 H 2 A,B 5 5 4 0 9 1 0.733 2 I 2 G,H 3 2 4 3 4 2 0.3967 13 J 6 F 1 5 4 6 7 3 0.3739 14 K 1 C,E 3 3 2 4 5 1 0.3599 16 L 2 E,G,H 3 2 2 8 3 4 0.3621 15 M 4 I,K 2 2 2 2 4 8 0.2363 20 N 2 F,L 1 4 4 3 4 1 0.2657 19 O 3 L 5 5 4 6 2 3 0.7496 1 P 5 J,M,N 3 2 3 4 7 8 0.4276 12 Q 8 O 4 5 4 2 3 4 0.6221 5 R 2 D,O 5 3 3 3 7 8 0.6672 4 S 6 P,R 2 4 6 2 3 4 0.4619 10 T 2 Q 1 6 2 7 5 2 0.3135 18

Daily Resource Limit 7 10 10 16 18 13

Table 6 gives the information about the weighted sum of the activities and ranking the activities as per their weighted sum. Table 7 Arranging the Activities as per their Rank in the Ascending Order and Scheduling the Activities as per the Precedence Relationship

by Considering the Weighted Sum Ranking.

Rank Activity Predecessor Duration

(days) R1 R2 R3 R4 R5 R6 1 O L 3 5 5 4 6 2 3 2 H A,B 2 5 5 4 0 9 1 3 D - 6 5 4 3 5 5 4 4 R D,O 2 5 3 3 3 7 8 5 Q O 8 4 5 4 2 3 4 6 A - 6 5 2 2 2 7 4 7 G D 2 4 1 4 3 9 8 8 F C 5 4 1 4 9 2 5 9 B - 3 3 5 2 3 9 6 10 S P,R 6 2 4 6 2 3 4 11 E A,B 7 3 5 2 3 8 0 12 P J,M,N 5 3 2 3 4 7 8 13 I G,H 2 3 2 4 3 4 2 14 J F 6 1 5 4 6 7 3 15 L E,G,H 2 3 2 2 8 3 4 16 K C,E 1 3 3 2 4 5 1 17 C A 4 2 4 4 2 3 1 18 T Q 2 1 6 2 7 5 2 19 N F,L 2 1 4 4 3 4 1 20 M I,K 4 2 2 2 2 4 8

The Critical Path is D-A-G-C-F-J-M-P-S and the Project Duration is 44 days.

5.

Conclusions

The perceptive ability and methods to build sound decisions are concerned in the complex decision making circumstances in the project management. The project scheduling with the assist of Fuzzy Analytical Hierarchy Process in developing the weightages for the activities are ended in this paper and the corresponding project schedule is shown in this paper. This paper provides the basis for applications of Fuzzy AHP weightages in the project scheduling. The concluding project scheduling and the project duration are obtained from the Gantt chart. By using Fuzzy AHP approach the project duration is reduced by 6days.

6.

References

1. Ayag, Z. A fuzzy AHP –based simulation approach to concept evaluation in a NPD environment. IIE Transactions, 37, 827-842, 2005b.

2. Banaszak, Z.A., & Zaremba, M.B. Project- driven planning and Scheduling support for virtual manufacturing. Journal of Intelligent Manufacturing. 17(6), 641-651, 2006.

3. Bedworth, David D., Industrial Systems: planning, analysis, control. New York: The Ronald Press Company, 1973. 4. Blazewicz, J., Lenstra, J.K., & Rinnooy Kan, A.H.G. Scheduling subject to resource constraints: classification and

complexity. Discrete Applied Mathematics, 5(1), 11-24, 1983.

5. Brooks, George H., Algorithm for activity scheduling to satisfy constraints on resource availability, unpublished paper, September 17, 1963.

6. Cheng, C. H., & Mon, D. L. Evaluating weapon system by Analytical Hierarchy process based on fuzzy scales. Fuzzy set and systems, 63, 1-10, 1994.

7. C. Kahraman, U. Cebeci, Z. Ulukan "Multi-criteria supplier selection using fuzzy AHP", Logistic information Management. Volume 16. Number 6. pp. 382-394, 2003.

8. Demeulemeester, E.L., Herroelen W.S. and Elmaghraby S.E., optimal procedure for the discrete time/cost trade-off problem in project networks, European journal of Operations research Vol. 89, no.2 (March), pp. 355-365, 1996.

9. Elmaghraby, S.E., “resource allocation via dynamic programming in activity networks,” European journal of Operations research, vol. 64, pp. 199-215, 1993.

10. Elsayed, Elsayed A., “Algorithm for project scheduling with resource constraints,” International Journal of Production Research, 20, no. 1, 1963.

11. Frank, H., I.T. Frisch, R. Vanslyke and W.S. Chou, Optimal design of centralized computer networks, networks, 1(1), 43-58, 1971.

12. Hartmann, S. Project Scheduling under limited resources. Berlin: Springer 1999.

13. Hasgul, S., Saricicek, I., Ozkan, K., & Parlaktuna, O. Project-oriented task scheduling for mobile robot team. Journal of Intelligent Manufacturing, 20(2), 151-158, 2009.

14. Herroelen, W. Project Scheduling- Theory and practice. Production and Operations Management, 14(4), 413-432, 2005. 15. Hindelang, T.J., & Muth J.F., A dynamic programming algorithm for decision CPM networks. Operations research,

27(2), 225-241, 1979.

16. Kaufmann, A., & Gupta, M. M. Introduction to fuzzy arithmetic: theory and applications. New York: Van Nostrand Reinhold, 1985.

17. Kolisch, R., & Hartmann, S. Experimental investigation of heuristics for resource constrained project scheduling: An update. European Journal of Operational Research, 174(1), 23-37, 2006.

18. L. Zadeh, "Fuzzy sets", information control, vol 8, pp.338-53, 1965.

D A GB C H E F J I K L O N M R Q P T S 0 5 10 15 20 25 30 35 40 45 50 D G C E J K O M Q T

19. Lee, Y.-H., Kumara, S.R.T., & Chatterjee, K. Multiagent based dynamic resource scheduling for distributed multiple projects using a market mechanism. Journal of Intelligent Manufacturing, 14(5), 471-484, 2003.

20. Mason, Richard, “An adaptation of the Brook’s algorithm for scheduling projects under multiple resource constraints,” unpublished M.S.thesis, Arizona state University, 1970.

21. Name: * "PMO and Project Management Dictionary". Pmhut.com. Retrieved 2014-06-24 (2007-08-20).

22. Nasr, Nabil Z., “New algorithms for project scheduling under resource constraints,” unpublished M.S.thesis, Rutgers University, 1983.

23. Neumann, K., & Zhan, J. Heuristic foe the minimum project duration problem with minimal and maximal time lags under fixed resource constraints. Journal of Intelligent Manufacturing, 6(2), 145-154 (1995).

24. Oddi, A., Cesta, A., Policella, N, & Smith, S.F. Iterative flattening search for resource constrained scheduling. Journal of Intelligent Manufacturing, 21(1), 17-30, 2010.

25. Pritsker, A.A.B., Watters, L.J., & Wolfe, P.M., Multi-project scheduling with limited resources: a zero-one programming approach. Management Science, 16(1), 93-108, 1969.

26. Robinson, D.R., A dynamic programming solution to cost-time trade-off for CPM, Management science, vol. 22, 1975. 27. Rothfarb, B.H.Frank, D.M. Rosenbaum, K. Steiglitz and D.J. Kleitman, Optimal design of offshore natural gas pipeline

systems, Operations Research, 18(6), 992-1020, 1970.

28. Satty TL. How to make a decision: the Analytic Hierarchy Process. European Journal of Operational Research, North-Holland; 48:9-26, 1990.

29. Shue, L. T., & Zamani, R. Intelligent search method for project Scheduling Problems. Journal of Intelligent Manufacturing, 10(3), 279-288, 1999.

30. Tarek Hegazy, “optimization of resource allocation and leveling using Genetic algorithms” Journal of construction engineering and management, Vol. 125, ASCE, pp. 167-175, May/June 1999

31. T. L. Satty, "The analytic hierarchy process", New York: McGraw-Hill; 1981.

32. T. L. Satty, Decision making, Scaling and number crunching. Decision Science, 20, 404- 409, 1989.

33. Whitehouse, Gary E., and James R. Brown, “GENRES: An extension of Brook’s algorithm for Project Scheduling with Resource Constraints,” Computers and Industrial Engineering, 3 1979.