Observations on the Hyperbola, y2 = 14x2 + 16t, t >=0

Observations on the Hyperbola, y2 = 14x2 + 16t, t

>=0

2

14

2

16

,

0







x

t

y

t

G. Sumathi1, A. Niranjani2 1

Assistant Professor, 2M.Phil Scholar, PG and Research Department of Mathematics, Shrimati Indira Gandhi College, Trichy-2, Tamil Nadu, India.

Abstract: The binary quadratic equation

y

2



14

x

2



16

t representing hyperbola is considered for finding its integer solutions. A few interesting properties among the solutions are presented. Also, we present infinitely many positive integer solutions in terms of Generalized Fibonacci sequences of numbers, Generalized Lucas sequences of numbers.

Keywords: Binary Quadratic Integral Solutions, Generalized Fibonacci Sequences of Numbers, Generalized Lucas Sequences of Numbers, Integral Solutions.

AMS Mathematics Subject Classification:11D09 Notations



k

s



GF

_n

,

: Generalized Fibonacci Sequences of rank n.



k

s



GL

_n

,

: Generalized Lucas Sequences of rank n.



























2

2

1

,

m

n

I

n

t

_mn





6

]

)

5

(

)(

2

(

)

1

(

[

n

n

m

n

m

P

_nm











)

1

(

Pr

_n



n

n



1

2

)

1

(

,







mn

n

Ct

_mn



1



1

6







n

n

S

_n

I. INTRODUCTION

The binary quadratic equation of the form

y

2



Dx

2



1

where D non-square positive integer has been studied by various mathematics for its non-trivial integer solutions.

when D takes different integral values



1

,

2

,

4



. In

 

3

infinitely many Pythagorean triangles in each of which hypotenuse is four times the product of the generators added with unity are obtained by employing the

y

2



14

x

2



1

. In [5] a special Pythagorean

triangles is obtained by employing the integral solutions of

y

2



182

x

2



14

t.

In [6] different patterns of infinitely many Pythagorean triangles are obtained by employing the non-integral solutions of

4

14

2

2

_

_x

_

y

. In this context one may also refer [7,8]. These results have motivated us to search for the integral solutions of

II. METHOD OF ANALYSIS

Consider the binary quadratic equation,

y

2



14

x

2



16

t

,

t



0

(1)

with least positive integer solutions of (1) ,

14

),

4

(

15

),

4

(

4

₀

0



y



D



x

t t

To obtain the other solutions of (1), Consider the pellian equation is

1

14

2 2





x

y

(2) The initial solution of pellian equation is

15

(

4

)

~

),

4

(

4

~

0 0

t t

y

x





The general solution



x

_n

,

y

_n



of (2) is given by,

n

n

g

x

14

2

1

~

_

_,

n

n

f

y

2

1

~

_

where,

1 1

)

14

4

15

(

)

14

4

15

(













n n

n

f

g

_n



(

15



4

14

)

n1



(

15



4

14

)

n1

Applying Brahmagupta lemma between



x

₀

,

y

₀



and



x

~

_n

,

~

y

_n



the general solutions of equation (1) are found to be,

n t n

t

n

f

g

x

4

14

2

15

4

.

2

1





 (3)

n t n

t

n

f

g

y

.

4

2

14

4

2

15

1





 (4)

Thus (3) and (4) represent the non-zero distinct integer solutions of (1) The recurrence relation satisfied by the solution and are given by

x

n3



30

x

n2



x

n1



0

y

n3



30

y

n2



y

n1



0

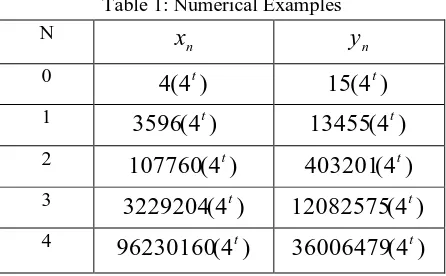
[image:2.612.195.418.571.709.2]

Some numerical examples of and satisfying (1) are given in the Table 1 below,

Table 1: Numerical Examples N

n

x

y

_n

0

₄

₍

₄

t

₎

)

4

(

15

t

1

₃₅₉₆

₍

₄

t

₎

)

4

(

13455

t

2

₁₀₇₇₆₀

₍

₄

t

₎

)

4

(

403201

t

3

_3229204

₍

₄

t

₎

)

4

(

12082575

t

4

_96230160

₍

₄

t

₎

)

4

(

A. A Few Interesting Relations Among The Solutions Are Given Below

1)

8

x

_n1



240

x

_n2



8

x

_n3



0

2)

1118

x

_n2



33750

x

_n1



8

y

_n1



0

3)

399842

x

n₁



13358

x

n₂



8

y

n₂



0

4)

30

x

_n1



898

x

_n2



8

y

_n3



0

5)

240

y

n₁



2

x

n₃



898

x

n₁



0

6)

30

x

_n1



30

x

_n3



240

y

_n2



0

7)

2

x

n₁



898

x

n₃



240

y

n₃



0

8)

30

x

_n2



2

x

_n1



8

y

_n2



0

9)

30

y

_n3



898

y

_n2



112

x

_n1



0

10)

1399080

x

_n1



374882

y

_n1



2

y

_n3



0

11)

30

x

_n2



2

x

_n3



8

y

_n2



0

12)

2

x

_n2



30

x

_n3



8

y

_n3



0

13)

30

x

n₃



898

x

n₂



8

y

n₁



0

14)

30

y

_n3



2

y

_n1



112

x

_n2



0

15)

30

y

n₃



30

y

n₁



3360

x

n₂



0

16)

2

y

n₃



30

y

n₂



112

x

n₂



0

17)

898

y

n₂



30

y

n₁



112

x

n₃



0

18)

898

y

_n3



2

y

_n1



3360

x

_n3



0

19)

448

y

_n1



13440

y

_n2



448

y

_n3



0

20)

112

x

_n3



30

y

_n1



898

y

_n2



0

B. Each Of The Following Expression Is A Nasty Number

1) _t

4

.

4

1

]

4

.

48

5388

180

[

x

_2n3



x

_2n2



t

2)

[

180

161460

1440

.

4

]

4

.

120

1

2 2 4

2

t n

n

t

x





x





3)

[

180

672

12

.

4

]

4

1

2 2 2

2

t n

n

t

y





x





4)

[

180

20160

180

.

4

]

4

.

15

1

2 2 3

2

t n

n

t

y





x





5) _t



3180

y

_n

604128

x

_n

3592

.

4

t



4

.

449

1

2 2 4

2 







6) _t



3592

x

_n

161460

x

_n

48

.

4

t



4

.

4

1

3 2 4

7) _t



3592

y

_n

672

x

_n

180

.

4

t



4

.

15

1

3 2 2

2 







8) _t



3592

y

_n

20160

x

_n

12

.

4

t



4

1

3 2 3

2 







9) _t



3592

y

_n

604128

x

_n

180

.

4

t



4

.

15

1

3 2 4

2 







10) _t



161460

y

_n

672

x

_n

3592

.

4

t



4

.

449

1

4 2 2

2 







11) _t



161460

y

_n

20160

x

_n

180

.

4

t



4

.

15

1

4 2 3

2 







12) _t



161460

y

_n

604128

x

_n

12

.

4

t



4

1

4 2 4

2 







13) _t



1440

y

_n

48

x

_n

48

.

4

t



4

.

4

1

3 2 2

2 







14) _t



43152

y

_n

48

y

_n

1440

.

4

t



4

.

120

1

4 2 2

2 







15) _t



43152

y

_n

1440

y

_n

48

.

4

t



4

.

4

1

4 2 3

2 







C. Each Of The Following Expressions Is A Cubical Integer

1)



898

_{3 3}

30

_{3 4}

2694

₁

90

₂



4

.

4

1

 







n



n



n

n

t

x

x

x

x

2)



30

_{3 5}

26910

_{3 3}

90

₃

80730

₁



4

.

120

1

 







n



n



n

n

t

x

x

x

x

3)



30

_{3 3}

112

_{3 3}

90

₁

336

₁



4

1

 







n



n



n

n

t

y

x

y

x

4)



30

_{3 4}

3360

_{3 3}

90

₂

10080

₁



4

.

15

1

 







n



n



n

n

t

y

x

y

x

5)



30

_{3 5}

100688

_{3 3}

90

₃

302064

₁



4

.

449

1

 







n



n



n

n

t

y

x

y

x

6)



898

_{3 5}

26910

_{3 4}

2694

₃

80730

₂



4

.

4

1

 







n



n



n

n

t

x

x

x

x

7)



898

_{3 3}

112

_{3 4}

2694

₁

36

₂



4

.

15

1

 







n



n



n

n

t

y

x

y

x

8)



898

_{3 4}

3360

_{3 4}

2694

₂

10080

₂



4

1

 







n



n



n

n

t

y

x

y

x

9)



898

_{3 5}

100688

_{3 4}

2694

₃

302064

₂



4

.

15

1

 







n



n



n

n

t

y

x

y

x

10)



26910

₃

112

_{3 5}

80730

₁

336

₃



4

.

449

1

 







n



n



n

n

11)



26910

_{3 4}

3360

_{3 5}

80730

₂

10080

₃



4

.

15

1

 







n



n



n

n

t

y

x

y

x

12)



26910

_{3 5}

100688

_{3 5}

80730

₃

302064

₃



4

1

 







n



n



n

n

t

y

x

y

x

13)



240

_{3 3\}

8

_{3 4}

720

₁

24

₂



4

.

4

1

 







n



n



n

n

t

y

y

y

y

14)



7192

_{3 3\}

8

_{2 5}

21576

₁

24

₃



4

.

120

1

 







n



n



n

n

t

y

y

y

y

15)



7192

_{3 4\}

240

_{3 5}

21576

₂

720

₃



4

.

4

1

 







n



n



n

n

t

y

y

y

y

D. Each Of The Following Expressions Is A Biquadratic Integer

1)

[

30

898

120

3592

24

.

4

]

4

.

4

1

2 2 3

2 4

4 5

4

t n

n n

n

t

x





x





x





x





2)

[

30

26910

120

107640

720

.

4

]

4

.

120

1

2 2 4

2 4

4 6

4

t n

n n

n

t

x





x





x





x





3) _t



30

y

_n

3360

x

_n

120

y

_n

13440

x

_n

90

.

4

t



4

.

15

1

2 2 3

2 4

4 5

4 















4) _t



30

y

_n

112

x

_n

120

y

_n

448

x

_n

6

.

4

t



4

1

2 2 2

2 4

4 4

4 















5) _t



30

y

_n

100688

x

_n

120

y

_n

402752

x

_n

2694

.

4

t



4

.

449

1

2 2 4

2 4

4 6

4 















6) _t



898

x

_n

26910

x

_n

3592

x

_n

107640

x

_n

24

.

4

t



4

.

4

1

3 2 4

2 5

4 6

4 















7) _t



898

y

_n

112

x

_n

3592

y

_n

448

x

_n

90

.

4

t



4

.

15

1

3 2 2

2 5

4 4

4 















8) _t



898

y

_n

3360

x

_n

3592

y

_n

13440

x

_n

6

.

4

t



4

1

3 2 3

2 5

4 5

4 















9) _t



898

y

_n

100688

x

_n

3592

y

_n

402752

x

_n

90

.

4

t



4

.

15

1

3 2 4

2 5

4 6

4 















10)





t n

n n

n

t

26910

y

112

x

107640

y

448

x

2694

.

4

4

.

449

1

4 2 2

2 6

4 4

4 















11) _t



26910

y

_n

3360

x

_n

107640

y

_n

402752

x

_n

90

.

4

t



4

.

15

1

4 2 4

2 6

4 5

4 















12) _t



240

y

_n

8

y

_n

960

y

_n

32

y

_n

24

.

4

t



4

.

4

1

3 2 2

2 5

4 4

4 















13) _t



7192

y

_n

8

y

_n

28768

y

_n

32

y

_n

720

.

4

t



4

.

120

1

4 2 2

2 6

4 4

4 















E. Each Of The Following Expression Is A Quintic Integer

1)



30

_{5 6}

898

_{5 5}

4490

_{3 3}

150

₄

8980

₁

300

₂



4

.

4

1

    





n



n



n



n



n

n

t

x

x

x

x

x

x

2)



30

_{5 7}

26910

_{5 5}

150

_{3 5}

134550

_{3 3}

300

₃

269100

₁



4

.

120

1

    





n



n



n



n



n

n

t

x

x

x

x

x

x

3)

_





















    

5 5 5 3 3 3 2 1 1

5

112

560

150

1120

300

30

4

1

n n n n n n

t

y

x

y

x

y

4)



480

₁

3360

_{5 5}

150

_{3 4}

16800

_{3 3}

33600

₁

150

₂



4

.

15

1

    





n



n



n



n



n

n

t

y

x

y

x

x

y

5)



30

_{5 7}

100688

_{5 5}

150

_{3 4}

503440

_{3 3}

300

₃

2013760

_1`



4

.

449

1

    





n





n



n



n

n

t

y

x

y

x

y

x

6)



898

_{5 5}

112

_{5 6}

4490

_{3 3}

560

_{3 4}

8980

₁

1120

₂



4

.

15

1

    





n



n



n



n



n

n

t

y

x

y

x

y

x

7)

_





















_{    }

7 5 6 3 5 3 4 3 2

5

26910

4490

134550

8980

269100

898

4

.

4

1

n n n n n n

t

x

x

x

x

x

x

8)



898

_{5 6}

3360

_{5 6}

4490

_{3 4}

16800

_{3 4}

8980

₂

33600

₂



4

1

    





n



n



n



n



n

n

t

y

x

y

x

y

x

9)



898

_{5 7}

100688

_{5 6}

4490

_{3 5}

503440

_{3 4}

8980

₃

2013760

₂



4

.

15

1

    





n



n



n



n



n

n

t

y

x

y

x

y

x

10)



26910

_{5 5}

112

_{5 7}

134550

_{3 3}

560

_{3 5}

269100

₁

2240

₃



4

.

449

1

    





n



n



n



n



n

n

t

y

x

y

x

y

x

11)



26910

_{5 6}

3360

_{5 7}

134550

₄

16800

_{3 5}

269100

₂

33600

₃



4

.

15

1

    





n



n



n



n



n

n

t

y

x

y

x

y

x

12)



26910

_{5 7}

100688

_{5 7}

134550

₅

503440

_{3 5}

269100

₃

2013760

₃



4

1

    





n



n



n



n



n

n

t

y

x

y

x

y

x

13)



240

_{5 5}

8

_{5 6}

1200

_{3 3}

40

_{3 4}

1320

₂

3640

₁



4

.

4

1

    





n



n



n



n



n

n

t

y

y

y

y

y

y

14)



7192

_{5 5}

8

_{5 7}

3596

_{3 3}

40

_{3 4}

104284

₁

80

₃



4

.

120

1

    





n



n



n



n



n

n

t

y

y

y

y

y

y

15)



7192

_{5 6}

240

_{5 7}

35960

_{3 4}

1200

_{3 5}

71920

₂

2400

₃



4

.

4

1

    





n



n



n



n



n

n

t

y

y

y

y

y

y

16) The solution of (1) in terms of special integers namely, generalized Fibonaci

n

GF

and Lucas

GL

_n are exhibited below,

)

1

,

30

(

)

4

(

60

)

1

,

30

(

)

4

(

2

_{1 1}

1













 n

t n

t

n

GL

GF

x

)

1

,

30

(

224

)

1

,

30

(

)

4

(

2

15

1 1

1













 t n n

n

GL

GF

III. REMARKABLE OBSERVATION

1) Employing linear combinations among the solutions of (1), one may generate integer solutions for other choices of hyperbola

which are presented in table 2 below

Table 2: Hyperbolas

2) Employing linear combination among the solutions of (1), one may generate integer solutions for other choices of parabolas which are presented in table 3 below

Table 3: Parabolas

S.NO Parabola (X,Y)

1 ₂

_{ }

2

4

8

56

4

t

X



Y



t



898

x

2n2



30

x

2n3

,

60

x

n1



2

x

n2



2

 

2

 

2

4

28800

14

4

120

t

X



Y



t



30

x

2n4



26910

x

2n2

,

7192

x

n1



8

x

n3



3

 

2

 

2

4

2

4

t

X



Y



t



112

x

2n2



30

y

2n2

,

30

x

n1



8

y

n1



4

 

2

 

2

4

403202

14

4

449

t

X



Y



t



30

y

2n4



100688

x

2n2

,

26910

x

n1



8

y

n3



5

 

2

 

2

4

32

14

4

4

t

X



Y



t



898

x

2n4



26910

x

2n3

,

7192

x

n2



240

x

n3



6

 

2

 

2

4

450

14

4

15

t

X



Y



t



30

y

2n3



3360

x

2n2

,

898

x

n1



8

y

n2



7

 

2

 

2

4

450

14

4

15

t

X



Y



t



898

y

2n2



112

x

2n3

,

30

x

n2



240

y

n1



8

 

2

 

2

4

2

14

4

t

X



Y



t



898

y

2n3



3360

x

2n3

,

898

x

n2



240

y

n2



9

 

2

 

2

4

450

14

4

15

t

X



Y



t



898

y

2n4



100688

x

2n3

,

26910

x

n2



240

y

n3



S.NO Hyperbola (X,Y)

1 2 2

 

2

4

64

224

Y

t

X









2 1

2

1

30

14

,

60

2

14

898

x

_n



x

_n

x

_n



x

_n

2 2 2

 

2

4

57600

14

Y

t

X







30

x

_n3



26910

X

_n1

,

7192

x

_n1



8

x

_n3



3 2 2

 

2

4

4

t

Y

X







112

x

_n1



30

y

_n1

,

30

x

_n1



8

Y

_n1



4 2 2

 

2

4

900

14

X

t

X







30

y

_n2



3360

x

_n1

,

898

x

_n1



8

y

_n2



5 2 2

 

2

4

806404

14

Y

t

X







30

y

n_3



100688

x

n_1

,

26910

x

n_1



8

y

n_3



6 2 2

 

2

4

64

14

Y

t

X







898

x

_n3



26910

x

_n2

,

7192

x

_n2



240

x

_n3



7 2 2

 

2

4

900

14

Y

t

X







898

y

n1



112

x

n2

,

30

x

n2



240

y

n1



8 2 2

 

2

4

4

14

Y

t

X







898

y

_n2



3360

x

_n2

,

898

x

_n2



240

y

_n2



9 2 2

 

2

4

900

14

Y

t

X







898

y

_n3



100688

x

_n2

,

26910

x

_n2



240

y

_n3



10 2 2

 

2

4

806404

14

Y

t

X







26910

y

_n1



112

x

_n3

,

30

x

_n3



7192

y

_n1



11 2 2

 

2

4

900

14

Y

t

X







26910

y

_n2



3360

x

_n3

,

898

x

_n3



7192

y

_n2



12 2 2

 

2

4

4

14

Y

t

X







26910

y

n_3



100688

x

n_3

,

26910

x

n_3



7192

y

n_3



13 2 2

 

2

4

12544

14

196

X



Y



t



240

y

_n1



8

y

_n2

,

30

y

_n2



898

y

_n1



14 2 2

 

2

4

5644800

14

196

X



Y



t



7192

y

_n1



8

y

_n3

,

30

y

_n3



26910

y

_n1



15 2 2

 

2

4

200704

224

11

 

2

 

2

4

450

14

4

15

t

X



Y



t



26910

y

_2n3



3360

_2n4

,

898

x

_n3



7192

y

_n2



12

 

2

 

2

4

2

14

4

t

X



Y



t



26910

_2n4



100688

x

_2n4

,

26910

x

_n3



7192

y

_n3



13

 

2

 

2

4

5644800

14

4

25320

t

X



Y



t



7192

y

_2n2



8

y

_2n4

,

30

y

_n3



26910

y

_n1



14

 

2

 

2

4

6272

14

4

784

t

X



Y



t



240

y

_2n2



8

y

_2n3

,

30

y

_n2



898

y

_n1



15

 

2

 

2

4

448

4

56

t

X



Y



t



7192

y

_2n3



240

y

_2n4

,

898

y

_n3



26910

y

_n2



3) Employing the following solutions (x,y), each of the following expressions among the special polygonal, pyramidal, star, pronic and centered polygonal number is congruent to under modulo 16

2

1 3 2

2 , 3

2 3

Pr

84

3



































 



x x

y

y

P

t

P

2

2 3 2 2

1 5

1

504

1

12







































_



 x

X

y y

S

P

S

P

2

1 5 2

, 3

5

1

168







































x x

y y

S

P

t

P

2

, 6

5 2

, 4

5

84

1

2





































_x

x

y y

Ct

P

Ct

P

2

, 4

5 2

3 3

3

1

1848

4





































 

x x

n n

Ct

P

P

Pt

IV. CONCLUSION

To conclude, one may search for other choices of positive Pell equations for finding their integer solutions with suitable properties.

REFERENCES

[1] L.E.Dickson, History of Theory of numbers, Vol.2, Chelsea Publishing Company, New York,(1952) [2] L.J.Mordell, Diophantine Equations, Academic Press, New York, 1969.

[3] M.A.Gopalan and G.Janaki, Observation On

y

2



3

x

2



1

, Acta Ciancia Indica, XXXIVM(2) (2008) 639-696. [4] L.E.Dickson, History of Theory of numbers and Diophantine analysis, Vol 2, Dover publications, Newyork,(2005)

[5] Dr.G.Sumathi “Observations On the Hyperbola”

y

2



182

x

2



14

, Journal of mathematics and Informatics,Vol 11, 73-81, 2017.

[6] Dr.G.Sumathi “Observations on the Pell equation

y

2



14

x

2



4

”International Journal of Creative Research Thoughts, Vol 6, Issue 1,Pp1074-1084, March 2018.

[7] Dr.G.Sumathi “Observations on the Equation

y

2



312

x

2



1

” International Journal of Mathematics Trends and Technology, Vol 50, Issue4, 31-34, Oct 2017.