ORDERING GENERALIZED LR FUZZY NUMBERS

ORDERING GENERALIZED LR FUZZY

NUMBERS

Y.L.P. Thorani

GSIB, GITAM University, Visakhapatnam, Andhra Pradesh, India

thorani02@gmail.com

N.Ravi Shankar

Dept. of Applied Mathematics, GIS, GITAM University, Visakhapatnam,, Andhra Pradesh, India

drravi68@gmail.com

Abstract :

Ordering fuzzy numbers plays an important role in approximate interpretation, optimization, forecasting, decision making, scheming, arrangement and other usage. Numerous methods for ranking of fuzzy numbers are available in the existing literature, which have their own pitfalls in some aspects. In this paper, a new ranking method for ordering generalized LR fuzzy numbers from its λ- cut is proposed to overcome the undiscriminating nature of the available methods. The proposed ranking method is explained and compared with some of examples existing in the literature.

Keywords: Ranking function; Centroid; Generalized LR fuzzy numbers

.

1. Introduction

Ranking fuzzy numbers play an important role in decision making. A number of ranking approaches had been proposed for the ranking of fuzzy numbers. Yager (1981) proposed a ranking index for the LR fuzzy numbers from its λ- cut for ordering fuzzy sets. Liou and Wang (1992) introduced a method for ranking fuzzy numbers with integral values. Yao and Wu (2000) came up with the ranking method for ranking fuzzy numbers based on decomposition principle and signed distance. Abbasbandy and Asady (2006) , Asady and Zendehnam (2007) stated that a fuzzy number is mapped to a real number based on the area measurement. Abbasbandy and Hajjari (2009) introduced a ranking method for ranking fuzzy numbers based on the left and the right spreads at some α-levels of trapezoidal fuzzy numbers. But the existing methods had some drawbacks and limitations such as, they cannot rank generalized fuzzy numbers, crisp numbers which are special cases of fuzzy numbers and cannot discriminate fuzzy numbers when they are having equal ranks. To overcome the limitations of the existing studies and to simplify the computational procedures, In this paper a new ranking method i.e., Centroid of centroids from its

λ

-cut for linear and nonlinear reference functions to generalized LR fuzzy numbers is given and also uses mode and spreads in those cases where the discrimination is not possible and a comparative study is made with some of the existing ranking methods.

The rest of the paper is organized as follows: In section 2, preliminaries are given. In section 3, the new ranking method is given and an important result like linearity of ranking function which is the basis for defining the ranking procedure is discussed and proved in section 3.2. In section 4, comparative study of the proposed ranking method with the existing methods is given. Finally, the conclusion is given in section 5.

2. Preliminaries

Definition 1: A fuzzy number A~=

(

m,n,α,β

)

_LR is said to be an LR fuzzy number if

   

   

 

> ≥     

 ₋

> ≤     

 −

=

. ,

1

, 0 , ,

, 0 , ,

) (

~

otherwise n x n x R

m x x m L

x

A _β β

α α

where L and R are continuous, non-increasing functions that define the left and right shapes of

μ

_A~

(

x

)

respectively and L(0) = R(0) =1.

Linear reference functions and nonlinear reference functions with their inverses are presented in Table 1.

Table 1: Reference functions and their inverses

Definition 2: Let A~=

(

m,n,α,β

)

_LR be an LR fuzzy number and

λ

be a real number in the interval [0,1]. Then

the crisp set _λ =

{

∈ :μ~

( )

x ≥λ

}

=[m−αL−1

( )

λ ,n+βR−1

( )

λ ]

A X x

A is said to be λ-cut of

A~

.

3. New ranking approach to various linear and non-linear functions of LR fuzzy number from its

λ

-cut based on area, mode and spread.

In this section, new ranking approach is presented for the ranking of LR fuzzy numbers. This method involves a procedure for ordering fuzzy sets in which a ranking approach R(A~)is calculated for the fuzzy number

(

m n

)

LR

A~= , ,α,β from its'

λ

-cut

3.1 Proposed Ranking Method

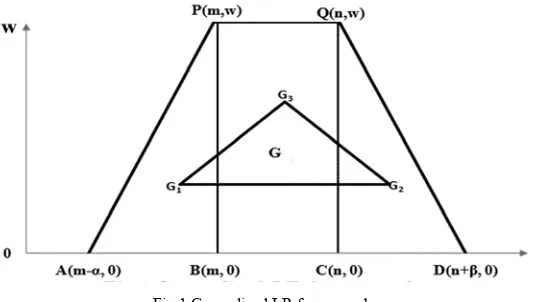
Generally, the Centroid is considered as the balancing point of a trapezoid . In this new ranking method the trapezoid (APQD) is divided into the triangle (APB), the rectangle (BPQC) and the triangle (CQD), and the centroids of these three plane figures APB, BPQC and CQD be G1, G2 and G3 respectively as shown in Fig. 1.

The centroid of the triangle (APB), where A = (m-α, 0), P = (m, w), C = (n, 0) is, 

  



 −

=

3 , 3 3

1 m w

G α

The centroid of the rectangle (BPQC), where B = (m, 0), P = (m, w), Q = (n, w), C = (n, 0), is, 

  



 +

=

2 , 2

2 m n w

G

The centroid of the triangle (QCD), where Q = (n, w), C = (n, 0), D = (n+β, 0) is, 

  



 +

=

3 , 3 3

3 n w

G β

Equation of the line G1G3 is y= w₃ and G2 does not lie on the line G1G3. Therefore G1, G2 and G3 are

non-collinear and they form a triangle.

The Centroid of the triangle (G1G2G3) is the intersection of the three centroid points G1, G2 and G3 as shown in

Fig.1. Since each Centroid point is a balancing point of each individual triangle, therefore Centroid of the triangle (G1G2G3) is taken as the better point of reference than the centroid pont of the trapezoid, as it is much

more balancing point, it is used to define the ranking of generalized LR fuzzy numbers A

(

m,n, , ;w

)

LR

~_{= α β .}

Function Name

Reference Function (RF) Inverse of Reference function α∈

(

0,1

]

Linear RF_p

( )

x ₌max

{

0,1 -x

}

_RF−1

( ) (

_{x = 1−α}

)

p

Exponential _RF

( )

_{x =e}−px_{, p≥1}

p RFp

( ) ( )

x In /p

1 _{=− α}

−

Power _RF

( )

_{x =max}

(

_01,−xp

)

_{, p≥}

p RF_p−1

( )

x = p1−α

Exponential

power

( )

= , ≥1

− _p

e x

RFp xp

( )

p

p x In

RF −1 = − α

Rational _RF

( )

_{x =1}

( )

_1+xp _{, p≥1}

Fig 1 Generalized LR fuzzy number

The Centroid G

( )

x y

A ,

~ of the triangle (G₁G₂G₃) with vertices G₁, G₂ and G₃ for the generalized trapezoidal LR

fuzzy number A

(

m,n, , ;w

)

LR

~ _{α β}

= is

( )



  



 + − +

=

18 7 , 18

2 2 9 9 ,

~ x y m n w

G A

β

α ₍₁₎

The Centroid G

( )

x y

A ,

~ of the triangle (G₁G₂G₃) with vertices G₁, G₂ and G₃ for the generalized triangular LR

fuzzy number A

(

m,n, , ;w

)

LR

~ _{α β}

= i.e., m = n is

( )



  



 − +

=

18 7 , 18

2 2 18 ,

~ x y m w

G A

β

α ₍₂₎

The ranking function of the generalized trapezoidal LR fuzzy number ~A=

(

m,n,α,β;w

)

_LR which maps the

set of all fuzzy numbers to a set of real numbers is defined as:

( )

(

)



  



 + − + _×

= × =

18 7 18

2 2 9 9

~ m n w

y x A

R α β (3)

This the Area between the Centroid of the Centroids G

( )

x y

A~ , as defined in Eq. (1) and the original point.

The ranking function of the generalized trapezoidal LR fuzzy number A

(

m,n, , ;w

)

LR

~ _{α β}

= of Eq. (1) from its

cut

−

λ

is defined as

( )

(

( )

)

(

( )

)

_

  

  

+ + −

= w



m αL− λ dλ



n βR− λ dλ

A R

1

0

1 1

0

1

2 9 2 9 2

) 18 (

7 2 ~

(4)

Since R

( )

A~ is calculated from the extreme values of λ-cut of A~, rather than its membership function, it is not

required knowing the explicit form of the membership functions of the fuzzy numbers to be ranked. That is unlike most of the ranking methods that require the knowledge of the membership functions of all fuzzy numbers to be ranked. This centroid of centroid index is still applicable even if the explicit form the membership function of the fuzzy numbers is unknown.

The ranking indexes for Eq. (4) for linear and nonlinear reference functions are:

( ) ( )

i Lx R

( )

x

{

x

}

Case = = max 0,1−

R

( )

A = w

[

9m+9n−α+β

]

) 18 (

14 ~

2

( ) ( ) ( )

_{ii Lx Rx e} x

Case = = −

( )

[

9 9 2α 2β

]

) 18 (

14 ~

2 + − +

= w m n

A R

( ) ( )

{

}

( )

x

e x R and x

L iii

Case = max0,1 -x = −

( )

[

9 9 α 2β

]

) 18 (

14 ~

2 + − +

= w m n

( ) ( )

iv L x e and R

( )

x

{

x

}

Case = −x = max 0,1−

( )

=

[

9

m

+

9

n

−

2

α

+

β

]

)

18

(

w

14

A~

R

₂

( ) ( )

_{v Lx e} px _{and R}

( )

_x

{

_xp

}

Case = − =max 0,1−

( )



  

 

+ + − + =

1 2 2 9 9 ) 18 (

14 ~

2 _p

p p n m w A

R α β

( ) ( )

{

p

}

( )

px

e x R and x x

L vi

Case = max 0,1− = −

( )



  

 

+ + − + =

p p

p n m w A

R α 2β

1 2 9 9 ) 18 (

14 ~

2

The Mode (M) of the generalized LR fuzzy number A

(

m,n, , ; w

)

LR

~ _{α β}

= is defined as:

M

( )

A

(

m n

)

dx w

(

m n

)

w

+ = +

=



0 2

2 1

~ ₍₅₎

The Spread (S) of the generalized LR fuzzy number A

(

m,n, , ;w

)

LR

~ _{α β}

= is defined as:

S

( )

A

(

n m

)

dx w

(

n m

)

w

− + + = − + +

=



α β α β

0

~ ₍₆₎

The Left spread (LS) of the generalized LR fuzzy number A

(

m,n, , ;w

)

LR

~ _{α β}

= is defined as:

( )

=



α = α w

w dx A

LS

0

~ ₍₇₎

The Right spread (RS) of the generalized LR fuzzy number

A~

=

(

m

,

n

,

α

,

β

;

w

)

_LR is defined as:

( )

=



β = β w

w dx A

RS

0

~

(8)

Working rule to find the ranks of two generalized LR fuzzy numbers

(

m n w

)

LR

A~₁ = ₁, ₁,α₁,β₁; _{1 and} A~₂ =

(

m₂,n₂,α₂,β₂; w₂

)

_LR, by using the ranking indexes for Eq. (4) for

linear and nonlinear reference functions, and using the equations from Eq. (5 )to Eq. (8), is defined as follows:

Step 1: Calculate R

( )

A~₁ andR

( )

A~₂

( )

i If R

( ) ( )

A~1 >RA~2 thenA~1 >A~2

( )

ii If R

( ) ( )

A~1 < RA~2 thenA~1 <A~2

( )

iii If R

( ) ( )

A~1 =RA~2 , then go to step 2.

Step 2: Calculate M

( )

A~₁ andM

( )

A~₂

( )

i If M

( ) ( )

A~1 >M A~2 then A~1 >A~2

( )

ii IfM

( ) ( )

A~1 <M A~2 then A~1<A~2

( )

iii IfM

( ) ( )

A~1 =M A~2 , then go to step 3. Step 3: Calculate S

( )

A~₁ and S

( )

A~₂

( )

i IfS

( ) ( )

A~1 > S A~2 then A~1 < A~2

( )

ii IfS

( ) ( )

A~1 < S A~2 then A~1 > A~2

( )

iii If S

( ) ( )

A~1 =S A~2 , then go to step 4.

Step 4: Calculate LS

( )

A~₁ and LS

( )

A~₂

( )

ii IfLS

( )

A~1 < LS

( )

A~2 then A~1<A~2

( )

iii If LS

( )

A~1 =LS

( )

~A2 , then go to step 5.

Step 5: Examine

w

₁

and

w

₂

( )

i If w1 >w2 then A~1 > A~2

( )

ii If w1<w2 then A~1 < A~2

( )

iii If w1= w2 thenA~1 ≈ A~2

3.2 Verification of Linear Properties of the New Ranking Function

In this Section, an important result which is the basis for defining the ranking procedure in Section 3.1 is discussed and proved.

Property 3.2.1.

The ranking function of centroid of centroids fron its

λ

−

cut

Eq. (4) is a linear function of the normal LR fuzzy number A

(

m,n, , ; w

)

LR

~_{= α β , i.e., if}

₍

₎

LR

w n

m

A_{1 1}, ₁, ₁, ₁; ₁

~ _{= α β and}

(

m n w

)

LR

A~₂ = ₂, ₂,α₂,β₂; ₂ are two normalized LR fuzzy numbers, then

( )

i R

(

k1A~1⊕k2A~2

)

=k1R

( )

~A1 ⊕k2R

( )

A~2

( )

ii R

( ) ( )

−A~ =−R A~

( )

iii R

(

( ) ( )

A~ ⊕ −A~

)

=0 where k1 and k2 are real numbers.

(i) Let k1, k2 be two real numbers

(

k1A~1⊕k2A~2

)

= (k1m1 + k2m2, k1n1 + k2n2, k1α1 + k2α2, k1β1 + k2β2)

By substituting

(

k1A~1⊕k2A~2

)

in Eq. (4) i.e., the ranking function for the centroid of centroids from its

cut

−

λ

, the following is obtained,

(

)

(

) (

) ( ) (

) (

) ( )

        ⊕ ⊕ ⊕ ⊕ ⊕ Θ ⊕ = ⊕



− − 1 0 1 2 2 1 1 2 2 1 1 1 2 2 1 1 2 2 1 1 2 2 2 1

1 9 2 9 2

) 18 ( 14 ~ ~ _{α α λ β β λ} R k k n k n k L k k m k m k A k A k R

( )

( )

( )

( )

_       + + Θ +         + + Θ =





− − − − 1 0 1 2 2 1 2 2 2 2 1 0 1 1 1 1 1 1 2 1 ) 2 9 2 9 ( ) 18 ( 14 ) 2 9 2 9 ( ) 18 ( 14 λ λ β λ α λ λ β λ α d R n L m k d R n L m k

=k1R

( )

A~1 ⊕k2R

( )

A~2

∴ R

(

k1~A1⊕k2A~2

)

=k1R

( )

A~1 ⊕k2R

( )

A~2

(ii) Let A~=

(

m,n,α,β;1

)

_LR and −A~=

(

−β,−α,−m,−n;1

)

By substituting A~ in Eq. (3.4)

( )

A

(

βR

( )

λ αL

( )

λ n m

)

dλ

R− =



− − + − − −

1

0

1 1

2 2 2 9 9

) 18 ( 14 ~ =

(

( )

( )

)

_       + − + −



− − 1 0 1 1

2 9 9 2 2

) 18 (

14 _{α λ β λ λ}

d R L

n m

∴R

( )

−A~ = −R

( )

A~

= R

( ) ( )

A~ ΘR A~ by (ii)

= 0

4

. Comparison of the New Ranking Method with the Existing Methods

Example 1

Set 1 with two fuzzy numbers from Chu and Tsao (2002), A~ =

(

2,2,0.1,0.1;1

)

_LRand B~=

(

3,3,0.9,1;1

)

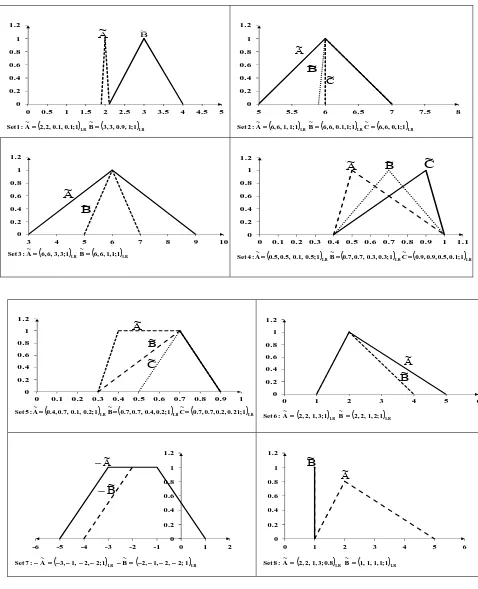
_LR,

as shown in Fig. 2. By using various ranking indexes for linear and nonlinear reference functions as defined in Section 3, the ranking order of A~and B~ in all the cases is A~<B~, the ranking results by the proposed method

is given in Table 3. From Fig.2 of set 1, it can be seen that the result obtained by our approach is reliable with human instinct. However, by the CV index proposed by Cheng (1998), the ranking order is A~ >B~, which is

unreasonable.

Example 2

Set 2 with three fuzzy numbers from Abbasbandy and Asady (2006) ,

(

6,6, ,11;1

)

,

~

LR

A= B~ =

(

6,6,0.1,1;1

)

_LR, and C~ =

(

6,6,0,1;1

)

_LRas shown in Fig 2. By using various

ranking indexes for linear and nonlinear functions reference as defined in Section 3, the ranking order of A~, B~and C~ in all cases is C~>B~ >A~ . The ranking results by the proposed method is given in Table 3.

However, by Chu and Tsao (2002), the ranking order is B~>C~>A~. Cheng (1998), proposed CV index,

through his approach the ranking order is A~ >B~ >C~. From Fig. 2, of set 2, it is easy to see that the ranking

results obtained by the existing approaches Chu and Tsao (2002) and Cheng (1998) are unreasonable and are not consistent with human instinct. On the other hand, by Abbasbandy and Asady (2006), the ranking results is

A B

C~> ~ > ~, which is the same as the one attained by our approach. However, the proposed approach is simpler

in the calculation.

Example 3

Set 3 with two fuzzy numbers from Chen and Lu (2002), A~ =

(

6,6,3,3;1

)

_LR , B~=

(

6,6,1,1;1

)

_LRas shown

in Fig. 2. By using various ranking indexes for linear and nonlinear reference functions as defined in Section 3, the ranking order of A~and B~ in case(i-ii) is R

( ) ( )

A~ =RB~ therefore by using Eq. (6) the result is obtained as

B

A~ > ~ and in case (iii-vi) the ranking order is A~ >B~, the ranking results by the proposed method is given in

Table 3. Because fuzzy numbers A~and B~have the same mode and symmetric spread, most of the existing

approaches fail. Yao and Wu (2000), Chu and Tsao (2002), Asady and Zendehnam (2007), Wang and Lee (2008) and get the same ranking order as A~≈B~. From Abbasbandy and Asady (2006), the ranking order of

fuzzy numbers is A~ ≈B~ and A~ >B~ for different index values i.e., when p = 1 and p = 2 respectively. By

Wang et al. (2005), the ranking order is A~ >B~. Tran-Duckein (2002) get the variance results when D_max and

Dmin are used respectively. Yao and Lin (2000), Liu (2001), Matarazzo and Munda (2001), approaches gave

different ranking order when different indices of optimism are taken. But by the new ranking approach the ranking results are same in all the cases i.e.,A~>B~.

Example 4

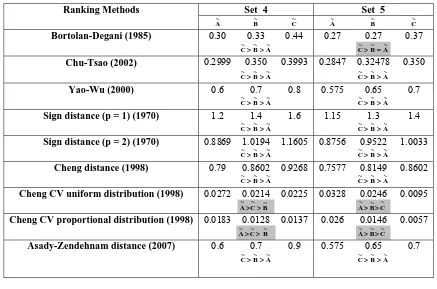
Consider two sets set 4 and set 5 with three fuzzy numbers from Yao and Wu (2000), as shown in Fig. 2.

(

0.5,0.5,0. ,10.5;1

)

, ~

(

0.7,0.7,0.3,0.3;1

)

~

(

0.9,0.9,0.5,0.1;1

)

.

~ :

4 A _LR B _LR andC _LR

Set = = = By using various

ranking indexes for linear and nonlinear reference functions as defined in Section 3, the ranking order of A~, B~and C~ in all the cases is C~>B~> A~. The ranking results by the proposed method is given in Table 3. The

ranking result by the proposed method and the ranking results of the existing methods Bortolan and Degani (1985), Yao and Wu (2000), Chu and Tsao (2002), Tran-Duckein (2002), the ranking order is C~>B~> A~

(

0.4,0.7,0.1,0.2;1

)

, ~

(

0.7,0.7,0.4,0.2;1

)

~

(

0.7,0.7,0.2,0.2;1

)

. ~

:

5 A _LR B _LR and C _LR

Set = = = By using

various ranking indexes for linear and nonlinear reference functions as defined in Section 3, the ranking order of

A~, B~and C~ in al cases is C~>B~> A~ . The ranking results by the proposed method is given in Table 3. The

ranking results of other approaches are given in Table 2. By Bortolan-Degani (1985) the ranking order is

A B

C~> ~ = ~ and by the CV index (Cheng (1998)), the ranking order is A~>B~>C~ , both the ranking orders is

counter-intuition (set 5 of Fig. 2).

Table 2: Comparative results of Example 4

Note: “ ” indicatesincorrect ranking results

Example 5

Set 6 with two fuzzy numbers from Liou and Wang (1992),A~=

(

2,2, ,13;1

)

_LR , B~=

(

2,2,1,2;1

)

_LR as shown

in Fig. 2. By using various ranking indexes for linear and nonlinear reference functions as defined in Section 3, the ranking order of A~and B~ in all the cases is A~ >B~, the ranking results by the proposed method is given in

Table 3. Liou and Wang (1992) obtained the different ranking order when different optimistic indices are adopted. Chu and Tsao (2002) approach obtain the ranking order as A~ >B~ which is same as the proposed

ranking method. But the proposed ranking method is simpler in the computation procedure. By Deng et al. (2006) the ranking order is A~< B~. A~ > B~ is more consistent with human intuition can be concluded from

Fig. 2 of set 6.

Example 6

Set 7, the images of set 6

(

3, ,1 2, 2 ;1

)

,

~

LR

A= − − − −

− B

(

2, ,1 2, 2;1

)

LR

~

− − − − =

− as shown in Fig. 2.

By using various ranking indexes for linear and nonlinear reference functions as defined in Section 3, the ranking order of −A~and −B~ in all the cases is −A~ <−B~, the ranking results by the proposed method is given

in Table 3. From set 6 and set 7, A~>B~ −A~<−B~Therefore the proposed ranking method can rank images

also.

Ranking Methods Set 4 Set 5 A~ B~ C~ A~ B~ C~ Bortolan-Degani (1985) 0.30 0.33 0.44 0.27 0.27 0.37

A~ B~

C~> > C~>B~=A~

Chu-Tsao (2002) 0.2999 0.350 0.3993 0.2847 0.32478 0.350 A~

B~

C~> > C~>B~>A~

Yao-Wu (2000) 0.6 0.7 0.8 0.575 0.65 0.7 A~

B~

C~> > C~>B~>A~

Sign distance (p = 1) (1970) 1.2 1.4 1.6 1.15 1.3 1.4 A~

B~

C~> > C~>B~>A~

Sign distance (p = 2) (1970) 0.8869 1.0194 1.1605 0.8756 0.9522 1.0033 A~

B~

C~> > C~>B~>A~

Cheng distance (1998) 0.79 0.8602 0.9268 0.7577 0.8149 0.8602 A~

B~

C~> > C~>B~>A~

Cheng CV uniform distribution (1998) 0.0272 0.0214 0.0225 0.0328 0.0246 0.0095 B~

C~

A~> > A~>B~>C~

Cheng CV proportional distribution (1998) 0.0183 0.0128 0.0137 0.026 0.0146 0.0057 B~

C~

A~> > A~>B~>C~

Asady-Zendehnam distance (2007) 0.6 0.7 0.9 0.575 0.65 0.7 A~

B~

Example 7

Consider set 8 with two fuzzy numbers A~ =

(

2,2, ,13;0.8

)

_LR , B~ =

(

,11,1,1;1

)

_LR as shown in Fig. 2. By using

various ranking indexes for linear and nonlinear reference functions as defined in Section 3, the ranking order of A~and B~ in all the cases is A~ >B~, the ranking results by the proposed method is given in Table 3.

Therefore, the proposed ranking method can rank fuzzy numbers with different heights and it can rank crisp numbers also. Yager (1981), cannot rank generalized LR fuzzy numbers.

Fig. 2: Eight sets of fuzzy numbers

0 0.2 0.4 0.6 0.8 1 1.2

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

A~ B~

( )LRB (3,3,0.9,1;1)LR

~ 1 ; 1 . 0 , 1 . 0 , 2 , 2 A ~ : 1

Set = =

0 0.2 0.4 0.6 0.8 1 1.2

5 5.5 6 6.5 7 7.5 8

A~

B~ C~

( )LR ( )LRC (6,6,0,1;1)LR

~ 1 ; 1 , 1 . 0 , 6 , 6 B~ 1 ; 1 , 1 , 6 , 6 A~ : 2

Set = = =

0 0.2 0.4 0.6 0.8 1 1.2

3 4 5 6 7 8 9 10

A~

B~

( )LRB (6,6,1,1;1)LR ~ 1 ; 3 , 3 , 6 , 6 A~ : 3

Set = =

0 0.2 0.4 0.6 0.8 1 1.2

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1

A~ B~ C~

( )LR ( )LRC (0.9,0.9,0.5,0.1;1)LR

~ 1 ; 3 . 0 , 3 . 0 , 7 . 0 , 7 . 0 B~ 1 ; 5 . 0 , 1 . 0 , 5 . 0 , 5 . 0 A~ : 4

Set = = =

0 0.2 0.4 0.6 0.8 1 1.2

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

A~

B~

C~

( )LR ( )LRC (0.7,0.7,0.2,0.21;1)LR

~ 1 ; 2 . 0 , 4 . 0 , 7 . 0 , 7 . 0 B~ 1 ; 2 . 0 , 1 . 0 , 7 . 0 , 4 . 0 A~ : 5

Set = = =

0 0.2 0.4 0.6 0.8 1 1.2

0 1 2 3 4 5 6

A~ B~

( )LR B (2,2,1,2;1)LR

~ 1 ; 3 , 1 , 2 , 2 A~ : 6

Set = =

0 0.2 0.4 0.6 0.8 1 1.2

-6 -5 -4 -3 -2 -1 0 1 2 A~

−

B ~

−

( )LR B (2, 1, 2, 2;1)LR

~ 1 ; 2 , 2 , 1 , 3 A~ : 7

Set − = − − − − − = − − − −

0 0.2 0.4 0.6 0.8 1 1.2

0 1 2 3 4 5 6

A~ B

~

( )LRB (1,1,1,1;1)LR

~ 8 . 0 ; 3 , 1 , 2 , 2 A~ : 8

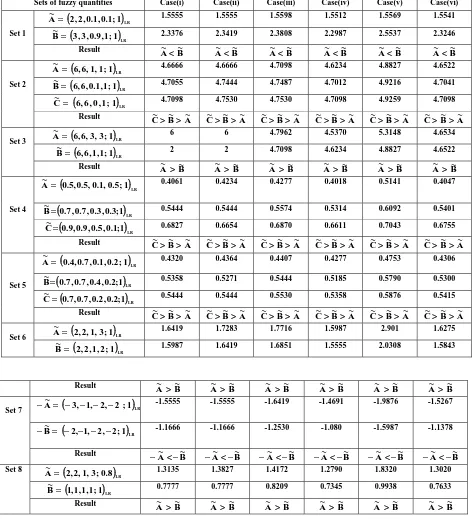
Table 3: Ranking results of the proposed ranking method

Sets of fuzzy quantities Case(i) Case(ii) Case(iii) Case(iv) Case(v) Case(vi)

Set 1

(

2,2,0.1,0.1;1

)

LR

A~= 1.5555 1.5555 1.5598 1.5512 1.5569 1.5541

(

3,3,0.9,1;1

)

LR

B~= 2.3376 2.3419 2.3808 2.2987 2.5537 2.3246

Result _A~ _<B~ _A~ _<B~ _A~_<B~ _A~_<B~ _A~ _<B~ _A~_<B~

Set 2

(

6,6,1,1;1

)

LR

A~ = 4.6666 4.6666 4.7098 4.6234 4.8827 4.6522

(

6,6,0.1,1;1

)

LR

B~= 4.7055 4.7444 4.7487 4.7012 4.9216 4.7041

(

6,6,0,1;1

)

LR

C~ = 4.7098 4.7530 4.7530 4.7098 4.9259 4.7098

Result _C~_>B~_>A~ _C~_>B~_>A~ _C~_>B~_>A~ _C~_>B~_>A~ _C~_>B~_>A~ _C~_>B~_>A~

Set 3 A

(

6,6,3,3;1

)

LR

~

= 6 6 4.7962 4.5370 5.3148 4.6534

(

6,6,1,1;1

)

LR

B~= 2 2 4.7098 4.6234 4.8827 4.6522

Result _A~ _>B~ _A~ _>B~ _A~ _>B~ _A~ _>B~ _A~ _>B~ _A~ _>B~

Set 4

(

0.5,0.5,0.1,0.5;1

)

LR

A~= 0.4061 0.4234 0.4277 0.4018 0.5141 0.4047

(

0.7,0.7,0.3,0.3;1

)

LR

B~= 0.5444 0.5444 0.5574 0.5314 0.6092 0.5401

(

0.9,0.9,0.5,0.1;1

)

LR

C~= 0.6827 0.6654 0.6870 0.6611 0.7043 0.6755

Result _C~_>B~_>A~ _C~_>B~_>A~ _C~_>B~_>A~ _C~_>B~_>A~ _C~_>B~_>A~ _C~_>B~_>A~

Set 5

(

0.4,0.7,0.1,0.2;1

)

LR

A~= 0.4320 0.4364 0.4407 0.4277 0.4753 0.4306

(

0.7,0.7,0.4,0.2;1

)

LR

B~= 0.5358 0.5271 0.5444 0.5185 0.5790 0.5300

(

0.7,0.7,0.2,0.2;1

)

LR

C~= 0.5444 0.5444 0.5530 0.5358 0.5876 0.5415

Result _C~_>B~_>A~ _C~_>B~_>A~ _C~_>B~_>A~ _C~_>B~_>A~ _C~_>B~_>A~ _C~_>B~_>A~

Set 6 A

(

2,2,1,3;1

)

LR

~

= 1.6419 1.7283 1.7716 1.5987 2.901 1.6275

(

2,2,1,2;1

)

LR

B~= 1.5987 1.6419 1.6851 1.5555 2.0308 1.5843

Result _A~ _>B~ _A~ _>B~ _A~ _>B~ _A~ _>B~ _A~ _>B~ _A~ _>B~

Set 7 A

(

3, 1, 2, 2;1

)

LR

~

− − − − =

− -1.5555 -1.5555 -1.6419 -1.4691 -1.9876 -1.5267

(

2, 1, 2, 2;1

)

LR

B~= − − − −

− -1.1666 -1.1666 -1.2530 -1.080 -1.5987 -1.1378

Result _−A~ _<−B~ _−A~_<−B~ _−A~ _<−B~ _−A~ _<−B~ _−A~ _<−B~ _−A~_<−B~

Set 8

(

)

LR

8 . 0 ; 3 , 1 , 2 , 2

A~= 1.3135 1.3827 1.4172 1.2790 1.8320 1.3020

B

(

1,1,1,1;1

)

LR

~

= 0.7777 0.7777 0.8209 0.7345 0.9938 0.7633

Result _A~ _>B~ _A~ _>B~ _A~ _>B~ _A~ _>B~ _A~ _>B~ _A~ _>B~

6. Conclusion

In this paper, a new method for ranking generalized LR fuzzy numbers to various linear and non-linear functions of generalized LR fuzzy numbers from its λ-cut based on area, mode and spread is presented. The proposed ranking method can efficiently rank various generalized LR fuzzy numbers, their images and crisp numbers which are considered to be a special case of fuzzy numbers and can overcome the limitations and shortcomings of the existing methods and the proposed method is relatively simple in computation and is easily logical and agrees with human intuition. The proposed method can be applied in real life problems.

References

[1] Abbasbandy, S. and Asady, B. (2006) : Ranking of fuzzy numbers by sign distance, Information Sciences, Vol.176, pp. 2405-2416.

[3] Asady, B. and Zendehnam, A.(2007): Ranking fuzzy numbers by distance minimization, Applied Mathematical Modelling, Vol. 31,

pp. 2589-2598.

[4] Bortolan, G. and Degani, R.(1985) :A review of some methods for ranking fuzzy subsets, Fuzzy Sets and Systems,Vol. 15, pp. 1-19.

[5] Chen, L.H. and Lu, H.W.(2002) :The preference order of fuzzy numbers, Computers and Mathematics with Applications, Vol. 44, pp.

1455-1465.

[6] Cheng, C.H.(1998): A new approach for ranking numbers by distance method, Fuzzy Sets and Systems, Vol. 95, pp. 307-317.

[7] Chu, T.C. and Tsao, C.T.(2002):Ranking fuzzy numbers with an area between the centroid point and original point, Computers and Mathematics with Applications, Vol. 43, No. (1/2), pp. 111-117.

[8] Deng,Y., Zhu, Z.F. and Liu, Q.(2006): Ranking fuzzy numbers with an area method using Radius of Gyration, Computers and Mathematics with Applications, Vol. 5143, No. (1/2),pp. 111-117.

[9] Lious, T.S.and Wang, M.J.(1992): Ranking fuzzy numbers with integral value, Fuzzy Sets and Systems, Vol. 5, pp. 247-255.

[10] Liu, X.(2001): Measuring the satisfaction of constraints in fuzzy linear programming, Fuzzy Sets and Systems, Vol. 122, pp. 263-275.

[11] Matarazzo, B. and Munda, G.(2001): New approaches for the comparison of L-R fuzzy numbers: a theoretical and operational analysis, Fuzzy Sets and Systems, Vol. 118, pp.407-418.

[12] Tran, L.and Duckein, L.(2002): Comparison of fuzzy numbers using a fuzzy distance measure, Fuzzy Sets and Systems, Vol. 35, pp.

331-341.

[13] Wang, M.L., Wang, H.F. and Lung, L.C.(2005) :Ranking fuzzy number based on lexicographic screening procedure, International Journal of Information Technology and Decision Making, Vol. 4, pp. 663-678.

[14] Wang, Y.J. and Lee, S.H.(2008):The revised method of ranking fuzzy numbers with an area between thecentroid and original points,

Computers and Mathematics with Applications, Vol. 55, pp. 2033-2042.

[15] Yager, R. R.(1981): A procedure for ordering fuzzy subsets of the unit interval, Information Sciences, Vol. 24, pp.143-161.