IMPROVED JOB-GROUPING BASED
PSO ALGORITHM FOR TASK
SCHEDULING IN GRID COMPUTING
MRS.S.SELVARANI
Department of Information Technology, Tamilnadu College of Engineering, Coimbatore, India DR.G.SUDHA SADHASIVAM
Department of Computer Science and Engineering, PSG College of Technology, Coimbatore, India
Abstract:
The goal of grid computing is to provide powerful computing abilities for complicated tasks by using all available and free computational resources. A suitable and efficient scheduling algorithm is needed to schedule user jobs to heterogeneous resources distributed in the grid. So scheduling is an important issue in a grid computing environment. In this paper an improved heuristic approach based on Particle Swarm Optimization (PSO) algorithm is presented to solve task scheduling problem in grid.
In this proposed scheduling approach tasks are grouped and allocated in an Un-uniform manner. The percentage of the processing capability of a resource on the total processing capability of all the resources is calculated. Using this percentage, the processing capability of a resource based on the total length of all tasks to be scheduled is calculated. Due to job grouping this approach optimizes computation/communication ratio and the utilization of resources is also increased.
Keywords: task scheduling, Particle Swarm Optimization, grid computing
1. Introduction:
The popularity of the Internet and the availability of powerful computers and high-speed networks as low-cost commodity components are changing the way we use computers today. These technical opportunities have led to the possibility of using geographically distributed and multi-owner resources to solve large-scale problems in science, engineering, and commerce. Recent research on these topics has led to the emergence of a new paradigm known as Grid computing [4].
To achieve the promising potentials of tremendous distributed resources, effective and efficient scheduling algorithms are fundamentally important. Unfortunately, scheduling algorithms in traditional parallel and distributed systems, which usually run on homogeneous and dedicated resources, e.g. computer clusters, cannot work well in the new circumstances [2].
Task scheduling is a challenging problem in grid computing environment [4]. A good scheduling algorithm must be used to schedule large number of computing tasks on the geographically distributed and multiowner resources.New challenges in Grid computing still make it an interesting topic, and many research projects are interested in this problem. This is due to the characteristics of Grids and the complex nature of the problem itself.
The static scheduling algorithms Minimum Execution Time, Minimum Completion Time, Min-min,
Max-minand XSuffrage are usually used to schedule applications that consist of a set of independent coarse-grained compute-intensive tasks. This is the ideal case for which the computational Grid was designed. But there are some other cases in which applications with a large number of lightweight jobs. The overall processing of these applications involves a high overhead cost in terms of scheduling and transmission to or from Grid resources. Muthuvelu et al [10] propose a dynamic task grouping scheduling algorithm to deal with these cases.
Most task scheduling problems belong to the class of NP-complete problems; so many researchers have
turned their attention to population based searching techniques like PSO. To solve NP-Complete problems a number of heuristic optimization techniques like simulated annealing(SA), Genetic Algorithm(GA)and Tabu searchhave been presented by Abraham, R. Buyya and B. Nath [1].
PSO is one of the latest population-based search models and has been applied successfully to a number of optimization problems [4]. A PSO algorithm contains a swarm of particles in which each particle includes a potential solution.
In cellular manufacturing systems, job grouping has been used to enhance efficiency of machinery utilization as mentioned by Logendran, Carsom and Hanson[7]. Similarly Gerasoulis and Yang [5], in the context of Directed Acyclic Graph (DAG) scheduling in parallel computing environments, named grouping of jobs to reduce communication dependencies among them as clustering. As presented by Muthuvelu and Liu [9] a job grouping mechanism was used to reduce the job assignment overhead.
Grouping the user jobs have been conducted at GRIDS laboratory Melbourne University using GridSim toolkit [9]. In this simulation, user jobs were grouped based on each resource’s processing capacity which is measured in Million Instructions per Second (MIPS). PSO for task scheduling in Grid Computing was proposed by Lei/Zhang and Yuchu Chen [8].
We propose an improved PSO algorithm where user jobs were grouped in an Un-uniform manner. This is done based on the percentage of a particular resource processing capacity on the total processing capacity of all the resources available in the grid, which improves computation/communication ratio and utilization of resources, It also reduces the makespan.
Through a number of simulated experiments, we prove that the proposed PSO algorithm with job grouping utilizes the available resources more efficiently and also reduces the communication time.
The rest of the paper is organized as follows: Grid scheduling problem issues are discussed in Section 2. Section 3 introduces the proposed improved PSO algorithm with job grouping. Experiments settings and results are discussed in Section 4. Finally conclusions are presented in Section 5.
2. Grid scheduling problem issues
Computational Grids are among the first type of Grid systems. They were developed due to the need to solve problems that require processing a large quantity of operations or data.
A resource is a basic computational entity (computational device or service) where tasks, jobs and applications are scheduled, allocated and processed accordingly. Resources have their own characteristics such as CPU characteristics, memory, software, etc.
Our aim is to “Find a task-resource mapping instance such that the estimated total execution time is minimized and the utilization of the resources is effective”.
To formulate the problem, define Ti i ={1,2,3,…n} as n independent tasks permutation and Rj
j={1,2,3,…m} as m computing resources with an objective of minimizing the completion time and utilizing the resources effectively. The processing capacity of each resource is expressed in MIPS (Machine Instructions per second) and the size of each task in MI (Number of Machine Instructions). Suppose that the processing time Pi,j
for task i computing on j resource is known. The completion time Ttot(x) represents the sum of the total
computation time Texe(x) and total communication time Tcomm(x) (Equation 1). Total computation time is
calculated by adding the processing time of all the resources (Equation 2).
Ttot(x) = Texe(x) + Tcomm(x) (1)
n m
Where Texe(x) = Σ Σ Pi,j (2)
i=1 j=1
In our problem, optimization criteria are minimization of makespan and minimization of flowtime. Makespan indicates the time when finishes the latest task and flowtime is the sum of finalization times of all the tasks. Formally they can be defined as:
Minimization of makespan:
Minimization of flowtime:
{∑ }
Where Tj denotes the time when task j finalizes, Sched is the set of all possible schedules and Tasks the set of all jobs to be scheduled.
Maximizing the resource utilization of the Grid system is another important objective. One possible definition of this parameter is to consider the average utilization of resources. For a schedule S, it can be defined as follows:
∑ (3)
where Total time(i) is the time of completion of resource and m is the total number of resources, and we aim at maximizing this value over all possible schedules.
An optimal schedule will be the one that optimizes makespan, flowtime and resource utilization. To reduce the total completion time the computation time and the communication time must be reduced.
In our proposed algorithm, instead of sending each job one at a time to the available resources, they will be sent after grouping them according to the processing capabilities of various resources in the grid. So the proposed algorithm optimizes makespan, flowtime and resource utilization.
3. Proposed Improved PSO algorithm with Un-uniform job grouping
3.1 Methodology
The scheduler accepts number of tasks, average MI of tasks, deviation percentage of MI granularity size and
processing overhead of all the tasks. The resources are selected. The processing capability of all the resources is calculated by adding the processing capability of all the selected resources (Tot-MIR), which is denoted as _ ∑ _ (4)
To utilize the resources effectively and to distribute the jobs to all the available resources, the processing capability of a resource on the total processing capability of all the resources is calculated (PTot-MIj), which is
denoted as
_ ∑ _ / _ (5)
Using this value the processing capability of a resource based on the total length of all tasks to be scheduled is calculated (PTot-GMIj), which is denoted as
_ ∑ _ _ (6)
Now tasks are grouped according to the availability of the processing capabilities of the resources as calculated above and submitted to the resources for computation, thereby resources are utilized effectively.
3.2 Particle Swarm Optimization for scheduling
Particle Swarm Optimization (PSO) is a swarm-based intelligence algorithm [6] influenced by the social
behaviour of animals such as a flock of birds, finding a food source or a school of fish protecting themselves from a predator. A particle in PSO is analogous to a bird or fish flying through a search (problem) space. The movement of each particle is co-ordinated by a velocity which has both magnitude and direction. Each particle position at any instance of time is influenced by its best position and the position of the best particle in a problem space. The performance of a particle is measured by a fitness value, which is problem specific.
The PSO algorithm is similar to other evolutionary algorithms [6]. In PSO, the population is the number of particles in a problem space. Particles are initialized randomly. Each particle will have a fitness value, which will be evaluated by a fitness function to be optimized in each generation. Each particle knows its best position pbest and the best position so far among the entire group of particles gbest. The pbest of a particle is the best result (fitness value) so far reached by the particle, whereas gbest is the best particle in terms of fitness in an entire population. In each generation the velocity is updated using equation 7 and the position of particles will be updated using equation 8.
vik+1 = ωvik + c1rand1 × (pbesti − xik) +c2rand2 × (gbest − xik) (7)
xik+1 = xik + vik+1 (8)
Where:
vik : velocity of particle i at iteration k
vik+1 : velocity of particle i at iteration k + 1
ω : inertia weight
randi : random number between 0 and 1; i = 1, 2
xik : current position of particle i at iteration k
pbesti : best position of particle i
gbest : position of best particle in a population xik+1 : position of the particle i at iteration k + 1.
PSO algorithm.
Step 1: Set particle dimension as equal to the size of ready tasks in {ti} T
Step 2: Initialize particles position randomly from Rj j={1,2,3,…m} and velocity vi
randomly.
Step 3: For each particle, calculate its fitness value as in Equation 1
Step 4: If the fitness value is better than the previous best pbest, set the current fitness value as the new pbest.
Step 5: After Steps 3 and 4 for all particles, select the best particle as gbest.
Step 6: For all particles, calculate velocity using Equation 7 and update their positions using Equation 8.
Step 7: If the stopping criteria or maximum iteration is not satisfied, repeat from Step 3.
The algorithm starts with random initialization of particle’s position and velocity. In this problem, the particles are the task to be assigned and the dimension of the particles is the number of tasks in a workflow. The value assigned to each dimensions of a particles are the computing resources indices. Thus the particles represent a mapping of resource to a task. The evaluation of each particle is performed by the fitness function given in Equation. 1. The particles calculate their velocity using Equation 3 and update their position according to Equation 4. The evaluation is carried out until the specified number of iterations (user-specified stopping criteria). PSO algorithm provides a mapping of all the tasks to a set of given resources based on the processing capability of the available resources.
3.3 Improved job grouping algorithm
Terms used in the algorithm
n : Total number of gridlets
m : Total number of Resources available Gi : List of Gridlets submitted by the user
Rj : List of Resources available
MI : Million instructions or processing requirements of a user job
MIPS : Million instructions per second or processing capabilities of a resource Tot-Jleng : Total processing requirements (MI) of a Gridlet group (in MI) Tot-MIj : Total processing capability (MI) of jth resource
Tot-MIR : Total processing capability of all the available resources ( Sum of the processing capabilities of all the available resources )
PTot-MIj : processing capability of jth resource on the total processing capability of
all the available resources which is calculated as Tot-MIj / Tot-MIR
PTot-GMIj : processing capability of the jth resource on the total length of all
Gridlets available which is calculated as PTot-MIj * Tot-GMI
Rj-MIP : MIPS of jth Grid resource
Gi-MI : MI of ith Gridlet
Tot-GMI : Total length of all gridlets (MI)
Granularity Size : Granularity size (time in seconds) for job grouping GJk : List of Grouped Gridlets
TargetRk : List of target resources of each grouped job
Algorithm
Step 1 : The scheduler receives Number of Gridlets ‘n’ and Number of Resources ‘m’ Step 2 : Scheduler receives the Resource-list R[ ]
Step 3 : Set Tot-MIR (Sum of the processing capacity of all the resources) to zero Step 4 : Set Tot-GMI (Sum of the length of all the gridlets) to zero
Step 6 : Set the resource ID j to 1 and the index i to 1
Step 7 : While j is less than or equal to m repeat steps 7.1 to 7.4 7.1: Get the jth resource from the resource list
7.2: Multiply the MIPS of jth resource with granularity time specified by the user
7.3: Find Tot-MIR by adding previous Tot-MIR with the value got from step 7.2 7.4: Get the MIPS of the next resource
Step 8 : While i is less than or equal to n repeat steps 8.1 to 8.3 8.1: Get the length of the ith Gridlet (G
i-MI)
8.2: Find Tot-GMI by adding previous Tot-GMI and Gi-MI
8.3: Get the length of the next Gridlet
Step 9 : While j is less than or equal to m repeat steps 9.1 to 9.3
9.1: calculate the processing capability of jth resource by multiplying MIPS of jth resource
and granularity time
9.2: calculate the processing capability of jth resource on the processing capability of all
the available resources(PTot-GMIj) by dividing processing capability of jth resource
by Tot-MIR
9.3: calculate the processing capability of jth resource on the total length of all available
gridlets by multiplying PTot-GMIj and Tot-GMI
Step 10: set k to zero
Step 11: While i is less than or equal to n repeat 12 to 14 Step 12: While j is less than or equal to m repeat steps 12.1 to 14 12.1: set Tot-Jleng to zero
12.2: while Tot-Jleng is less than equal to PTot-GMIj and i is less than n repeat
begin
calculate Tot-Jleng by adding previous Tot-Jleng and length of the ith Gridlet
(Gi-MI)
end
Step 13: if Tot-Jleng is greater than PTot-GMIj then
begin
subtract Gi-MI (length of the last Gridlet) from Tot-Jleng
end
Step 14: If Tot-Jleng is not zero repeat steps 14.1 to 14.4
14.1: Create a new Grouped-gridlet of length equal to Tot-Jleng 14.2: Assign a unique ID to the newly created Grouped-gridlet 14.3: Insert the Grouped-gridlet into a new Grouped-gridlet list GJk 14.4: Insert the allocated resource ID into the Target resource list TargetRk 14.5: Increment the value of k
Step 15: When all the gridlets are grouped and assigned to a resource, send all the Grouped- gridlets to their corresponding resources
Step 16: After the execution of the grouped-gridlets by the assigned resources send them back to the Target resource list
Step 17: Display the Id of the resource, start time, end time, simulation time and task execution cost of each executed grouped-gridlet
Number of user jobs and the number of resources available are submitted to the scheduler. User jobs are also submitted to the scheduler. Total processing capability of all the available resources is calculated (in MIPS). Total length (in MI) of all the tasks is calculated (Sum of the length of all the submitted tasks).
The percentage of the processing capability of a resource on the total processing capability of all the resources is calculated. Using this percentage, the processing capability of a resource based on the total length of all tasks to be scheduled is calculated. By this way the jobs are allocated to the available resources not uniformly, but the utilization of resources will be increased
Algorithm for Task scheduling using PSO with improved job grouping
Step 1 : The scheduler receives Number of Gridlets ‘n’ and Number of Resources ‘m’ Step 2 : Scheduler receives the Resource-list R[ ]
Step 3 : Set Tot-MIR (Sum of the processing capacity of all the resources) to zero Step 4 : Set Tot-GMI (Sum of the length of all the gridlets) to zero
Step 5 : The Gridlets created by the system are submitted to the scheduler Step 6 : Set the resource ID j to 1 and the index i to 1
Step 7 : While j is less than or equal to m repeat steps 7.1 to 7.4 7.1: Get the jth resource from the resource list
7.2: Multiply the MIPS of jth resource with granularity time specified by the user
7.3: Find Tot-MIR by adding previous Tot-MIR with the value got from step 7.2 7.4: Get the MIPS of the next resource
Step 8: Assign the gridlets to the resources using PSO algorithm Step 9 : While i is less than or equal to n repeat steps 9.1 to 9.3 9.1: Get the length of the ith Gridlet (G
i-MI)
9.2: Find Tot-GMI by adding previous Tot-GMI and Gi-MI
9.3: Get the length of the next Gridlet
Step 10 : While j is less than or equal to m repeat steps 10.1 to 10.3
10.1: calculate the processing capability of jth resource by multiplying MIPS of jth resource
and granularity time
10.2: calculate the processing capability of jth resource on the processing capability of all
the available resources(PTot-GMIj) by dividing processing capability of jth resource
by Tot-MIR
10.3: calculate the processing capability of jth resource on the total length of all available
gridlets by multiplying PTot-GMIj and Tot-GMI
Step 11: set k to zero
Step 12: While i is less than or equal to n repeat 13 to 15 Step 13: While j is less than or equal to m repeat steps 13.1 to 15 13.1: set Tot-Jleng to zero
13.2: while Tot-Jleng is less than equal to PTot-GMIj and i is less than n repeat
begin
calculate Tot-Jleng by adding previous Tot-Jleng and length of the ith Gridlet (G
i-MI)
end
Step 14: if Tot-Jleng is greater than PTot-GMIj then
begin
subtract Gi-MI (length of the last Gridlet) from Tot-Jleng
end
Step 15: If Tot-Jleng is not zero repeat steps 15.1 to 15.4
15.1: Create a new Grouped-gridlet of length equal to Tot-Jleng 15.2: Assign a unique ID to the newly created Grouped-gridlet 15.3: Insert the Grouped-gridlet into a new Grouped-gridlet list GJk 15.4: Insert the allocated resource ID into the Target resource list TargetRk 15.5: Increment the value of k
Step 16: When all the gridlets are grouped and assigned to a resource, send all the Grouped- gridlets to their corresponding resources
Step 17: After the execution of the grouped-gridlets by the assigned resources send them back to the Target resource list
Step 18: Display the Id of the resource, start time, end time, simulation time and task execution cost of each executed grouped-gridlet
5. Experimental Results
GridSim has been used to create the simulation environment [11]. The inputs to the simulations are total
Resource MIPS
R1 25 R2 52 R3 93 R4 322 R5 173 R6 291 R7 252 R8 304 Table 1 : MIPS of Grid Resources
The MIPS of the resources is computed by multiplying the Total Processing elements in each resource by the MIPS of each processing element in the resource and the Processing cost is computed by multiplying Total CPU time for task execution and cost per second of the resources.
We have experimented the above algorithms and obtained results for task scheduling with uniform job grouping using PSO and with Un-uniform job grouping using PSO. We have compared the time of execution, cost and utilization of resources for both the above algorithms.
a) Comparison of simulation time to complete task execution with uniform job grouping using PSO and with Un-uniform job grouping using PSO
Simulations were conducted to analyze and compare the above algorithms in terms of processing time. Figure 1 shows a column chart for comparing the results of the above algorithms with average gridlet length of 10 MI, deviation percentage 10% and granularity size 10 seconds.
From the Figure it can be seen that the time taken to complete tasks with Un-uniform grouping using PSO is very less when compared with time taken to complete the tasks with uniform grouping using PSO
Figure 1. Comparison of simulation time of Un-uniform and uniform grouping
b) Comparison of costs of uniform job grouping using PSO and with Un-uniform job grouping using PSO Simulations were conducted to analyze and compare the above algorithms in terms of processing cost. Figure 2 shows a column chart for comparing the results of the above algorithms with average gridlet length of 10 MI, deviation percentage 10% and granularity size 10 seconds.
0 100 200 300 400 500
50 100 150 200 250 300
Ti
me
in
sec
o
nds
Number of Gridlets
Uniform grouping
From the Figure it can be seen that the cost to complete tasks with Un-uniform grouping using PSO is very less when compared with time taken to complete the tasks with uniform grouping using PSO
Figure 2. Comparison of cost Un-uniform and uniform grouping
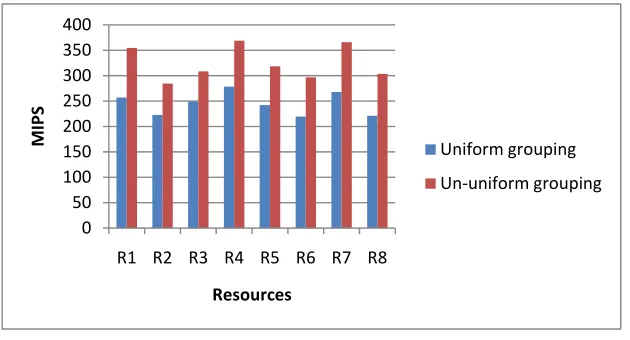
c) Comparison of resource utilization of uniform job grouping using PSO and with Un-uniform job grouping using PSO
Simulations were conducted to analyze and compare the above algorithms in terms of resource utilization for 200 gridlets. Figure 3 shows a column chart for comparing the results of the above algorithms with average gridlet length of 10 MI, deviation percentage 10% and granularity size 10 seconds.
From the Figure it can be seen that the utilization of resources is more when tasks are scheduled with Un-uniform grouping using PSO algorithm when compared with task scheduling with uniform grouping using PSO algorithm. Hence utilization of resources is maximized.
Figure 3. Utilization of resources for processing 200 gridlets
6. Conclusion
This paper discusses job scheduling using a Uniform-grouping of jobs using PSO. By doing research and
analysis of this problem, that aims at task scheduling with minimum total tasks completion time, minimum cost and maximization of utilization of resources. By using a new method to group the jobs, the above aims are achieved. GridSim is employed to carry out and simulate the tasks assignment algorithm, and distributed task
0 500 1000 1500 2000
50 100 150 200 250 300
Cost(Rs)
Number of Gridlets
Uniform grouping
Un‐uniform grouping
0 50 100 150 200 250 300 350 400
R1 R2 R3 R4 R5 R6 R7 R8
MIPS
Resources
Uniform grouping
scheduling .The results are compared with uniform grouping method. The conclusion is that the scheduling algorithm employed is better than the uniform grouping of jobs.
This proposed algorithm only takes the initial research on task scheduling in grid environment. However many issues remain open. Further improvement should be done to handle more complicated scenario involving dynamic factors such as dynamically changing grid environment and other QoS attributes. The improvement of this algorithm should concentrate on discussing simultaneous instead of independent task scheduling in heterogeneous grid computing environment
Acknowledgment
The authors convey their heartfelt thanks to Dr.C.Kalaiarasan, Principal, Tamilnadu College of Engineering, Coimbatore and Mr.K.V.Chidambaran, Director Cloud Computing Group, Yahoo Software Development (India) Pvt Ltd, Bangalore for providing them the required facilities to complete the project successfully. This project is carried out as a consequence of the PSG-Yahoo Research programme on Grid and Cloud computing References
[1] Abraham, R. Buyya and B. Nath, Nature's Heuristics for Scheduling Jobs on Computational Grids, The 8th IEEE International Conference on Advanced Computing and Communications (ADCOM 2000), pp. 45-52,Cochin, India, December 2000,.
[2] F. Berman, High-Performance Schedulers, chapter in The Grid: Blueprint for a Future Computing Infrastructure, edited by I. Foster and C. Kesselman, Morgan Kaufmann Publishers, 1998.
[3] R. Buyya and D. Abramson and J. Giddy and H. Stockinger, Economic Models for Resource Management and Scheduling in Grid
Computing, in J. of Concurrency and Computation: Practice and Experience, Volume 14, Issue.13-15, pp. 1507-1542, Wiley Press,
December 2002
[4] Foster and C. Kesselman (editors), The Grid: Blueprint for a Future Computing Infrastructure, Morgan Kaufman Publishers, USA, 1999.
[5] Gerasoulis, A. and Yang, T. (1992): A comparison of clustering heuristics for scheduling directed graphs on multiprocessors. Journal
of Parallel and DistributedComputing, 16(4):276-291
[6] J. Kennedy and R. C. Eberhard, “Particle swarm optimization”, Proc. of IEEE Int’l Conf. on Neural Networks, pp.1942-1948, Piscataway, NJ, USA, ,1995.
[7] Logendran, R., Carson, S. and Hanson, E. (2002): Group Scheduling Problems in Flexible Flow Shops. Proc. of the Annual
Conference of Institute of IndustrialEngineers, USA.
[8] Lei Zhang, Yuehui Chen and Bo Yang, 2006, “Task Scheduling Based on PSO Algorithm in Computational Grid”, Proceedings of the Sixth International Conference on Intelligent Systems Design and Applications (ISDA'06).
[9] Muthuvelu. N, Liu. J, Lin Soe. N, Venugopal. S, Sulistio. A and Buyya. R, 2005, “A Dynamic Job Grouping-Based Scheduling for Deploying Applications with FinGrained Tasks on Global Grids”, in Proc of Australasian Workshop on Grid Computing and e-Research (AusGrid2005), Feb. 2005, pp. 41-48.
[10] N. Muthuvelu, J. Liu, N. L. Soe, S.r Venugopal, A. Sulistio and R. Buyya, A Dynamic Job Grouping-Based Scheduling for Deploying
Applications with Fine-Grained Tasks on Global Grids, Proceedings of the 3rd Australasian Workshop on Grid Computing and
e-Research (AusGrid 2005), Newcastle, Australia, January 30 – February 4, 2005.
[11] Rajkumar Buyya, and Manzur Murshed, 2002, “GridSim: A Toolkit for the Modeling, and Simulation of Distributed Resource Management, and Scheduling for Grid Computing”, The Journal of Concurrency, and Computation: Practice, and Experience (CCPE), Vol 14, Issue 13-15, Wiley Press, USA, pp.1175-1220.
Authors Profile :
S.Selvarani received the B.E. degree in Computer Science and Engineering from Bharathiar University in 1991,
and M.E. degree in Computer Science and Engineering from Manonmaniam Sundaranar University in 2004. She is currently working toward the PhD degree in Computer Science and Engineering under Anna University, Coimbatore, India. Her research work is in Grid and Cloud Computing with techniques for resource management and task scheduling
Dr G Sudha Sadasivam is working as a Professor in Department of Computer Science and Engineering in PSG