Numerical Solution of First Order Fuzzy Differential
Equations by the Third Order Runge-Kutta Method Based
on Linear Combination of Arithmetic Mean, Geometric
Mean and Centroidal Mean
Gethsi Sharmila R
1, Suvitha S
2Assistant Professor1,2,
Department of Mathematics, Bishop Heber College, Tiruchirappalli, India. Email: gethsisharmila@gmail.com, suvithasobers@gmail.com
Abstract- In this paper, a numerical method for fuzzy differential equations based on Seikkala derivative of fuzzy process is applied. The numerical method used to solve the first order fuzzy differential equations is the third order Runge-Kutta method based on linear combination of Arithmetic Mean, Geometric Mean and Centroidal Mean. The efficiency of the proposed method is illustrated by solving first order fuzzy differential equations with Triangular Fuzzy Numbers and Trapezoidal Fuzzy Numbers. The results show that the proposed method suits well to find the numerical solution of Fuzzy Differential Equations.
Keywords: Fuzzy Differential Equations, Fuzzy Triangular Number, Fuzzy Trapezoidal Number, Runge-Kutta method, Arithmetic Mean, Geometric Mean, Centroidal Mean
1.
INTRODUCTIONThe research work on Fuzzy Differential Equations (FDEs) has been rapidly developing in recent years. Fuzzy Differential Equation models have wide range of applications in many branches of engineering and in the field of medicine. The concept of a fuzzy derivative was first introduced by Chang and Zadeh [6], later Dubois and Prade [7] defined the fuzzy derivative by using Zadeh’s extension principle and then followed by Puri and Ralescu [20]. Fuzzy differential equations have been suggested as a way of modelling uncertain and incompletely specified systems and were studied by many researchers [12,13]. The existence of solutions of fuzzy differential equations has been studied by several authors [4, 5]. It is difficult to obtain an exact solution for fuzzy differential equations and hence several numerical methods were proposed [14,15,17,18]. Abbasbandy and Allahviranloo [2] developed numerical algorithms for solving fuzzy differential equations based on Seikkala’s derivative of fuzzy process [21]. Runge-Kutta method for fuzzy differential equation has been studied by many authors [1, 19].
Abdul-Majid Wazwaz [3] introduced a comparison of modified Runge-Kutta formulas based on a variety of means. Evans and Yaacub [8] have introduced the fourth order Runge-Kutta method based on Centroidal Mean formula for first order IVPs. GethsiSharmila and Henry Amirtharaj introduced the
explicit third order weightedRunge-Kutta method and fourth order Runge-Kutta methodbased on Centroidal Mean [9,11] to solve IVPs and developed a numerical algorithm for finding the solution of Fuzzy Initial Value Problems by Fourth Order Runge-Kutta Method Based on Contraharmonic Mean [10].
In this paper, a new numerical method to solve first order linear fuzzy differential equations is presented using the third order Runge – Kutta method based on a linear combination of arithmetic mean, geometric mean and centroidal mean. The structure of the paper is organized as follows: In Section 2, some basic results on fuzzy numbers and fuzzy derivative are given. Then in Section 3 the fuzzy initial value problem is treated using the extension principle of Zadeh and the concept of fuzzy derivative.In Section 4, a third order Runge-Kutta method based on linear combination of arithmetic mean, Geometric mean and Centroidal mean is introduced. In Section 5 the proposed method is illustrated by solving two examples, and the conclusion is drawn in Section 6.
2. PRELIMINARIES
2.1 Definitions and Notations
The basic definition of fuzzy number is, if we denote the set of all real numbers by R and the set of all fuzzy numbers on R is indicated by RF then, a fuzzy number is a mapping such that 𝑢 : R → [0, 1], which satisfies the following four properties:
(i) 𝑢 is upper semi-continuous.
1. It is a bounded left continuous monotonic increasing function over [0, 1],
2. It is a bounded left continuous monotonic decreasing function over [0,1], and
3. A crisp number α is simply represented by
( )
( )
, 0
1.
u r
u r
r
Definition: 2.4 (Triangular Fuzzy Number):
A triangular fuzzy numberv, is defined by
three numbers
a
1
a
2
a
3where the graph of)
(
x
v
, the membership function of the fuzzy number v, is a triangle with base on the interval[
a a
1 ,]
3 and vertex at x = a2. We specify v as( /
a a a
1 2/ )
3 . The membership function for the triangular fuzzy number3. FUZZY CAUCHY PROBLEM
Consider the Fuzzy Initial Value Problem
{𝑦 ( ) ( 𝑦( ) ∈ , -
3.1.Runge – Kutta Method for Initial Value Problem Consider the initial value problem
( )
f ( , ( )) ; a
t
b
Equations (3.2) is to be exact for powers of h through m
h
, because it is to be coincident with Taylor series of order m.4. THE THIRD ORDER RUNGE – KUTTA
METHOD BASED ON A LINEAR
COMBINATION OF ARITHMETIC MEAN, GEOMETRIC MEAN, AND CENTROIDAL MEAN FOR FIRST ORDER DIFFERENTIAL EQUATION [ FRK3LCAMGMCEM ]
A new third order Runge – Kutta method based on a linear combination of Arithmetic Mean, Geometric Mean, and Centroidal Mean for first order Differential equation was proposed by using Khattri [16] as follows
( )
( ) ( ) ( )
For the IVP of the form y=f(t,y) the modified Third order Runge - Kutta methods using variety of means can be written in the form
𝑦 𝑦 [∑
]
Where means include Arithmetic Mean(AM), GeometricMean(GM),Contra – Harmonic Mean(CoM), Centroidal Mean (CeM), Root Mean Square (RM), Harmonic Mean(HaM), and Heronian Mean(HeM) which involves ki, 1
where, ( 𝑦 )
( 𝑦 ) ( 𝑦 )
substituting the Arithmetic Mean, Geometric Mean and Centroidal Mean, we have Geometric Mean, And Centroidal Mean For Fuzzy Differential Equations.
where the wi’s are constants and
1
where in the third order Runge-KuttaMethod based on linear combination of Arithmetic Mean, Geometric Mean andCentroidal Mean is as follows.
The solution is calculated by grid points at (3.2). By (4.1) and (4.5), we have the exact solution is given
5. NUMERICAL EXAMPLES
Example : 5.1(Triangular Number) Consider the Fuzzy Initial Value Problem
{ 𝑦 ( ) 𝑦( ) ∈ ,
-𝑦( ) ( )
The exact solution is obtained as
Y( )
y
( )Y
( )y
( )At t = 1, Y(1;r) = [(0.75+0.25r)e,(1.5-0.5r)e] The absolute error by the third order Runge-Kutta methodbased on a linear combination of Arithmetic Mean,GeometricMean and CentroidalMean for the r-level set with h=0.1 and t=1.0 of example 5.1 is givenin Table 5.1. The graphical representation for theapproximate solution ofFRK3LCAMGMCM and the exact solution of example 5.1 is given in figure.5.1.
Table 5.1(The approximate, exact and absolute error table for example 5.1 for r-level set with h=0.1 and t=1.0)
Figure 5.1. Comparison of the approximate solution with exact solutions of FRK3LCAMGMCeM for ex.4.1 when h=0.1 and t=1.
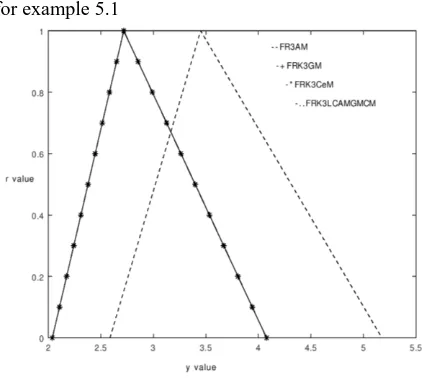
The comparison table of the absolute error of the proposed method with the existing methods for example 5.1 is given below.
Table 5.2 Comparison table of the absolute error for example 5.1
Figure 5.2. Comparison of the absolute error with the existing methods FRK3AM, FRK3GM, and FRK3CM for example 5.1
Example 5. 2
Consider the Fuzzy Initial Value Problem.
Y ( )
y
( )Y
(t;r) =y
(t;r)At t = 1, Y(1;r) = [(0.8+0.125r)e, (1.1-0.1r)e]
The absolute error by the third order Runge-Kutta method based on a linear combination of Arithmetic Mean ,Geometric Mean and Centroidal mean for the r-level set with h=0.1 and t=1.0 of example 5.2 is given in Table 5.3. The graphical representation for the approximate solution of FRK3LCAMGMCM and the exact solution of example 5.2 is given in figure.5.3 Table 5.2 The approximate, exact and absolute error table for example 4.1 for r- level set with h=0.1 and t=1.0
The approximate solution using FRK3LCAMGMCM with exact solution(h=0.1 & t=1)
The exact and approximate solutions are compared and plotted in figure (5.2).
7. CONCLUSION
In this paper, a new numerical method for solving first order fuzzy initial value problem is proposed. Here, the first order fuzzy differential equations is solved usingThe third order Runge-kutta method based on the linear combination of Arithmetic Mean,Geometric Mean and CentroidalMean. From the numerical examples, we could conclude that the proposed method almost coincides with the exact solution.
REFERENCES
[1] Abbasbandy. S, Allah Viranloo. T, Numerical
solution of fuzzy differential equations by
Runge-Kutta method, Nonlinear
studies.11(2004)N0.1,117-129.
[2] Abbasbandy. S, Allahviranloo. T, Numerical solution of fuzzy differential equations by Taylor method, Journal of Computational Methods and Applied Mathematics, 2(2002)113-124.
[3] Abdul-Majid Wazwaz, A comparision of modified Runge-Kutta formulas based on a variety of means, International Journal of Computer Mathematics, vol.50,pp-105-112.
[4] Balachandran. K, Prakash. P, Existence of solutions of fuzzy delay differential equations with nonlocal condition, Journal of the Korea Society for Industrial and Applied Mathematics, 6(2002)81-89.
[5] Balachandran. K, Kanagarajan. K, Existence of solutions of fuzzy delay integro-differential equations with nonlocal condition, Journal of the Korea Society for Industrial and Applied Mathematics, 9(2005)65-74.
[6] Chang. S.L, Zadeh. L.A, On fuzzy mapping and control, IEEE Trans, Systems Man Cybernet. 2(1972)30-34.
[7] Dubois. D, Prade. H, Towards fuzzy differential calculus part 3 : Differentiation, Fuzzy Sets and Systems, 8(1982)225-233.
[8] Evans, D.J. and Yaacub, A.R. (1993). A new fourth order Runge – Kutta Method based on the Centroidal Mean (CeM) formula. Computer Studies 851. Department of Computer Studies, University of Technology, Loughborough, U.K [9] GethsiSharmila .R and E.C. Henry Amirtharaj,
[10]GethsiSharmila.R and E.C. Henry Amirtharaj, Numerical Solution of Fuzzy Initial Value Problems by Fourth Order Runge-Kutta Method Based on Contraharmonic Mean, Indian journal of applied research 3(4) (2013) 339-343.
[11]GethsiSharmila.R and E.C. Henry Amirtharaj, Numerical Solution of Nth - Order Fuzzy Initial Value Problems by Fourth Order Runge-Kutta Method Basesd On Centroidal Mean IOSR Journal of Mathematics (IOSR-JM) Volume 6, Issue 3 (May. - Jun. 2013), PP 47-63
[12]Kaleva. O, Fuzzy differential equations, Fuzzy Sets and Systems, 24(1987)301-317.
[13]Kaleva. O, The Cauchy problem for fuzzy differential equations, Fuzzy Sets and Systems, 35(1990)389 -396.
[14]Kanagarajan. K, Sambath. M , Runge- Kutta Nystrom method of order three for solving fuzzy differential equations, Computational methods in Applied Mathematics, Vol.10(2010) , No.2, pp.195-203.
[15]Kanagarajan. K, Sambath. M ,Numerical solution of fuzzy differential equations by third order Runge-Kutta method , International journal of Applied Mathematics and Computaion , 2(4) (2010) pp.1-8.
[16]Khattri S.K.(2012),Euler’s Number and Some Means, Tamsui Oxford Journalof Information and Mathematical Sciences, pp369-377.
[17]Ma. M, Friedman. M, Kandel. A, Numerical solutions of fuzzy differential equations, Fuzzy Sets and Systems, 105(1999)133-138.
[18]Nirmala. V, Chenthur Pandian. S, “Numerical Solution of Fuzzy Differential Equation by Fourth Order Runge-Kutta Method with Higher Order Derivative Approximations”, European Journal of Scientific Research, Vol.62 N0.2 (2011),pp.198-206.
[19]Palligkinis. S.ch.,Papageorgiou. G, Famelis,I.TH., “Runge-Kutta methods for fuzzy differential equations”, App.Math.Comp 209(2009),97-105. [20]Puri. M.L, Ralescu. D.A, Differentials of fuzzy
functions, Journal of Mathematical Analysis and Applications, 91(1983)552-558.